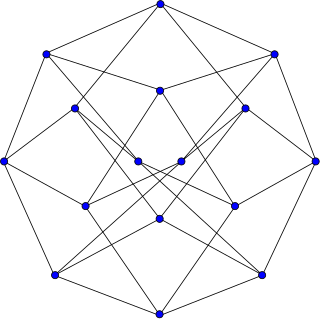
Blanuša snarks

Blanuša snarks
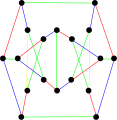
	The first Blanuša snark
Named after	Danilo Blanuša
Vertices	18 (both)
Edges	27 (both)
Radius	4 (both)
Diameter	4 (both)
Girth	5 (both)
Automorphisms	8, D4 (1st); 4, Klein group (2nd)
Chromatic number	3 (both)
Chromatic index	4 (both)
Book thickness	3 (both)
Queue number	2 (both)
Properties	Snark (both); Hypohamiltonian (both); Cubic (both); Toroidal (only one) [1]
	Table of graphs and parameters

Last updated March 14, 2019

In the mathematical field of graph theory, the Blanuša snarks are two 3-regular graphs with 18 vertices and 27 edges.^[2] They were discovered by Yugoslavian mathematician Danilo Blanuša in 1946 and are named after him.^[3] When discovered, only one snark was known—the Petersen graph.

Mathematics field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure, space, and change.

Graph theory study of graphs, which are mathematical structures used to model pairwise relations between objects

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices, nodes, or points which are connected by edges, arcs, or lines. A graph may be undirected, meaning that there is no distinction between the two vertices associated with each edge, or its edges may be directed from one vertex to another; see Graph for more detailed definitions and for other variations in the types of graph that are commonly considered. Graphs are one of the prime objects of study in discrete mathematics.

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other. A regular graph with vertices of degree $k$ is called a $k$ ‑regular graph or regular graph of degree $k$ . Also, from the handshaking lemma, a regular graph of odd degree will contain an even number of vertices.

In the mathematical field of graph theory, a snark is a simple, connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, the connectivity is redundant so that removing no one edge would split the graph, and the edges cannot be colored by only three colors without two edges of the same color meeting at a point. In order to avoid trivial cases, snarks are often restricted to have girth at least 5.

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.

In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.

Algebraic properties

The automorphism group of the first Blanuša snark is of order 8 and is isomorphic to the Dihedral group D₄, the group of symmetries of a square.

In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic. From the standpoint of group theory, isomorphic groups have the same properties and need not be distinguished.

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.

The automorphism group of the second Blanuša snark is an abelian group of order 4 isomorphic to the Klein four-group, the direct product of the Cyclic group Z/2Z with itself.

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, these are the groups that obey the axiom of commutativity. Abelian groups generalize the arithmetic of addition of integers. They are named after early 19th century mathematician Niels Henrik Abel.

In mathematics, the Klein four-group is a group with four elements, in which each element is self-inverse (composing it with itself produces the identity) and in which composing any two of the three non-identity elements produces the third one. It can be described as the symmetry group of a non-square rectangle (with the three non-identity elements being horizontal and vertical reflection and 180-degree rotation), as the group of bitwise exclusive or operations on two-bit binary values, or more abstractly as Z₂ × Z₂, the direct product of two copies of the cyclic group of order 2. It was named Vierergruppe (meaning four-group) by Felix Klein in 1884. It is also called the Klein group, and is often symbolized by the letter V or as K₄.

In group theory, the direct product is an operation that takes two groups $G$ and $H$ and constructs a new group, usually denoted $G \times H$ . This operation is the group-theoretic analogue of the Cartesian product of sets and is one of several important notions of direct product in mathematics.

The characteristic polynomial of the first and the second Blanuša snark are respectively :

In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix as coefficients. The characteristic polynomial of an endomorphism of vector spaces of finite dimension is the characteristic polynomial of the matrix of the endomorphism over any base; it does not depend on the choice of a basis. The characteristic equation is the equation obtained by equating to zero the characteristic polynomial.

(x-3)(x-1)^{3}(x+1)(x+2)(x^{4}+x^{3}-7x^{2}-5x+6)(x^{4}+x^{3}-5x^{2}-3x+4)^{2}\

(x-3)(x-1)^{3}(x^{3}+2x^{2}-3x-5)(x^{3}+2x^{2}-x-1)(x^{4}+x^{3}-7x^{2}-6x+7)(x^{4}+x^{3}-5x^{2}-4x+3).\

Generalized Blanuša snarks

There exists a generalisation of the first and second Blanuša snark in two infinite families of snarks of order 8n+10 denoted $B_{n}^{1}$ and $B_{n}^{2}$ . The Blanuša snarks are the smallest members those two infinite families.^[6]

In 2007, J. Mazák proved that the circular chromatic index of the type 1 generalized Blanuša snarks $B_{n}^{1}$ equals $3+{\frac {2}{n}}$ .^[7]

In 2008, M. Ghebleh proved that the circular chromatic index of the type 2 generalized Blanuša snarks $B_{n}^{2}$ equals $3+{\frac {1}{\lfloor 1+3n/2\rfloor }}$ .^[8]

Gallery

The chromatic number of the first Blanuša snark is 3.
The chromatic index of the first Blanuša snark is 4.
The chromatic number of the second Blanuša snark is 3.
The chromatic index of the second Blanuša snark is 4.

Related Research Articles

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In the mathematical field of graph theory, the butterfly graph is a planar undirected graph with 5 vertices and 6 edges. It can be constructed by joining 2 copies of the cycle graph C₃ with a common vertex and is therefore isomorphic to the friendship graph F₂.

Some of the finite structures considered in graph theory have names, sometimes inspired by the graph's topology, and sometimes after their discoverer. A famous example is the Petersen graph, a concrete graph on 10 vertices that appears as a minimal example or counterexample in many different contexts.

In the mathematical field of graph theory, the Pappus graph is a bipartite 3-regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic distance-regular graphs are known; the Pappus graph is one of the 13 such graphs.

In the mathematical field of graph theory, the Foster graph is a bipartite 3-regular graph with 90 vertices and 135 edges.

In graph theory, circular coloring may be viewed as a refinement of usual graph coloring. The circular chromatic number of a graph $, denoted can be given by any of the following definitions, all of which are equivalent.$

$is the infimum over all real numbers so that there exists a map from to a circle of circumference 1 with the property that any two adjacent vertices map to points at distance along this circle.$
$is the infimum over all rational numbers so that there exists a map from to the cyclic group with the property that adjacent vertices map to elements at distance apart.$
In an oriented graph, declare the imbalance of a cycle $to be divided by the minimum of the number of edges directed clockwise and the number of edges directed counterclockwise. Define the imbalance of the oriented graph to be the maximum imbalance of a cycle. Now, is the minimum imbalance of an orientation of .$

In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.

In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.

In the mathematical field of graph theory, the Franklin graph a 3-regular graph with 12 vertices and 18 edges.

In the mathematical field of graph theory, the Biggs–Smith graph is a 3-regular graph with 102 vertices and 153 edges.

In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.

In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.

In the mathematical field of graph theory, the double-star snark is a snark with 30 vertices and 45 edges.

In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.

In the mathematical field of graph theory, the Hoffman graph is a 4-regular graph with 16 vertices and 32 edges discovered by Alan Hoffman. Published in 1963, it is cospectral to the hypercube graph Q₄.

In the mathematical field of graph theory, the friendship graphF_n is a planar undirected graph with 2n+1 vertices and 3n edges.

In the mathematical field of graph theory, the Klein graphs are two different but related regular graphs, each with 84 edges. Each can be embedded in the orientable surface of genus 3, in which they form dual graphs.

References

↑ Orbanić, Alen; Pisanski, Tomaž; Randić, Milan; Servatius, Brigitte (2004). "Blanuša double". Math. Commun. 9 (1): 91–103.
↑ Weisstein, Eric W. "Blanuša snarks". MathWorld .
↑ Blanuša, D., "Problem cetiriju boja." Glasnik Mat. Fiz. Astr. Ser. II. 1, 31-42, 1946.
↑ Eckhard Steen, "On Bicritical Snarks" Math. Slovaca, 1997.
↑ Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
↑ Read, R. C. and Wilson, R. J. An Atlas of Graphs. Oxford, England: Oxford University Press, pp. 276 and 280, 1998.
↑ J. Mazák, Circular chromatic index of snarks, Master's thesis, Comenius University in Bratislava, 2007.
↑ M. Ghebleh, Circular Chromatic Index of Generalized Blanuša Snarks, The Electronic Journal of Combinatorics, vol 15, 2008.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Orbanić, Alen; Pisanski, Tomaž; Randić, Milan; Servatius, Brigitte (2004). "Blanuša double". Math. Commun. 9 (1): 91–103.

[2] Weisstein, Eric W. "Blanuša snarks". MathWorld .

[3] Blanuša, D., "Problem cetiriju boja." Glasnik Mat. Fiz. Astr. Ser. II. 1, 31-42, 1946.

[4] Eckhard Steen, "On Bicritical Snarks" Math. Slovaca, 1997.

[5] Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018

[6] Read, R. C. and Wilson, R. J. An Atlas of Graphs. Oxford, England: Oxford University Press, pp. 276 and 280, 1998.

[7] J. Mazák, Circular chromatic index of snarks, Master's thesis, Comenius University in Bratislava, 2007.

[8] M. Ghebleh, Circular Chromatic Index of Generalized Blanuša Snarks, The Electronic Journal of Combinatorics, vol 15, 2008.