
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable , or just distribution function of , evaluated at , is the probability that will take a value less than or equal to .

Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes . Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability theory describing such behaviour are the law of large numbers and the central limit theorem.

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

A random variable is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes in a sample space to a measurable space, often to the real numbers.
In probability theory, the central limit theorem (CLT) establishes that, in many situations, for identically distributed independent samples, the standardized sample mean tends towards the standard normal distribution even if the original variables themselves are not normally distributed.

A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs now." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov.

In probability and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value. Sometimes it is also known as the discrete density function. The probability mass function is often the primary means of defining a discrete probability distribution, and such functions exist for either scalar or multivariate random variables whose domain is discrete.

In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.
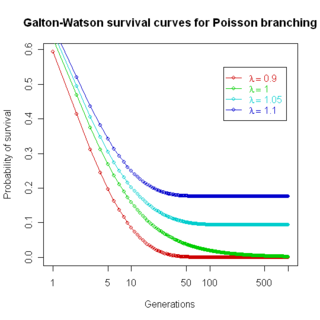
The Galton–Watson process is a branching stochastic process arising from Francis Galton's statistical investigation of the extinction of family names. The process models family names as patrilineal, while offspring are randomly either male or female, and names become extinct if the family name line dies out. This is an accurate description of Y chromosome transmission in genetics, and the model is thus useful for understanding human Y-chromosome DNA haplogroups. Likewise, since mitochondria are inherited only on the maternal line, the same mathematical formulation describes transmission of mitochondria. The formula is of limited usefulness in understanding actual family name distributions, since in practice family names change for many other reasons, and dying out of name line is only one factor.
In probability theory, a branching process is a type of mathematical object known as a stochastic process, which consists of collections of random variables. The random variables of a stochastic process are indexed by the natural numbers. The original purpose of branching processes was to serve as a mathematical model of a population in which each individual in generation produces some random number of individuals in generation , according, in the simplest case, to a fixed probability distribution that does not vary from individual to individual. Branching processes are used to model reproduction; for example, the individuals might correspond to bacteria, each of which generates 0, 1, or 2 offspring with some probability in a single time unit. Branching processes can also be used to model other systems with similar dynamics, e.g., the spread of surnames in genealogy or the propagation of neutrons in a nuclear reactor.
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its "true value". The error of an observation is the deviation of the observed value from the true value of a quantity of interest. The residual is the difference between the observed value and the estimated value of the quantity of interest. The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances.
In physics and mathematics, a random field is a random function over an arbitrary domain. That is, it is a function that takes on a random value at each point (or some other domain). It is also sometimes thought of as a synonym for a stochastic process with some restriction on its index set. That is, by modern definitions, a random field is a generalization of a stochastic process where the underlying parameter need no longer be real or integer valued "time" but can instead take values that are multidimensional vectors or points on some manifold.
In probability and statistics, memorylessness is a property of certain probability distributions. It usually refers to the cases when the distribution of a "waiting time" until a certain event does not depend on how much time has elapsed already. To model memoryless situations accurately, we must constantly 'forget' which state the system is in: the probabilities would not be influenced by the history of the process.
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.
In probability theory, Dirichlet processes are a family of stochastic processes whose realizations are probability distributions. In other words, a Dirichlet process is a probability distribution whose range is itself a set of probability distributions. It is often used in Bayesian inference to describe the prior knowledge about the distribution of random variables—how likely it is that the random variables are distributed according to one or another particular distribution.
In probability theory, the optional stopping theorem says that, under certain conditions, the expected value of a martingale at a stopping time is equal to its initial expected value. Since martingales can be used to model the wealth of a gambler participating in a fair game, the optional stopping theorem says that, on average, nothing can be gained by stopping play based on the information obtainable so far. Certain conditions are necessary for this result to hold true. In particular, the theorem applies to doubling strategies.
In physics, statistics, econometrics and signal processing, a stochastic process is said to be in an ergodic regime if an observable's ensemble average equals the time average. In this regime, any collection of random samples from a process must represent the average statistical properties of the entire regime. Conversely, a process that is not in ergodic regime is said to be in non-ergodic regime.
In probability theory and statistics, a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent. This property is usually abbreviated as i.i.d., iid, or IID. IID was first defined in statistics and finds application in different fields such as data mining and signal processing.
The Borel distribution is a discrete probability distribution, arising in contexts including branching processes and queueing theory. It is named after the French mathematician Émile Borel.






