
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.
In physics, a Langevin equation is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid.

In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities used in Lagrangian mechanics with (generalized) momenta. Both theories provide interpretations of classical mechanics and describe the same physical phenomena.
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain differential equations. The idea is to write the solution of the differential equation as a sum of certain "basis functions" and then to choose the coefficients in the sum in order to satisfy the differential equation as well as possible.

In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called canonical transformations, which map canonical coordinate systems into canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself as one of the new canonical momentum coordinates.
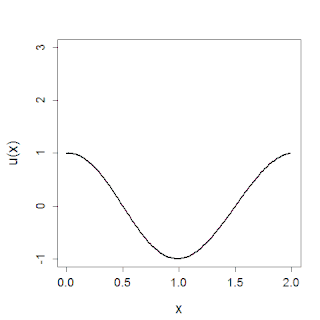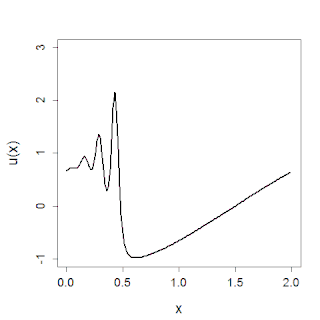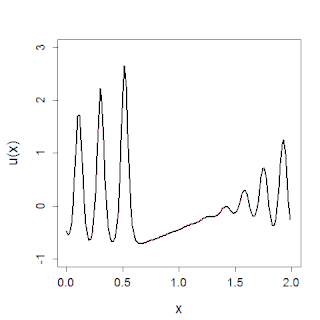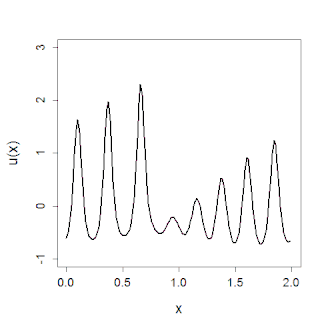
In mathematics, the Korteweg–De Vries (KdV) equation is a partial differential equation (PDE) which serves as a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an integrable PDE and exhibits many of the expected behaviors for an integrable PDE, such as a large number of explicit solutions, in particular soliton solutions, and an infinite number of conserved quantities, despite the nonlinearity which typically renders PDEs intractable. The KdV can be solved by the inverse scattering method (ISM). In fact, Gardner, Greene, Kruskal and Miura developed the classical inverse scattering method to solve the KdV equation.

The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.

In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic, cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.
In mathematics, a symplectic integrator (SI) is a numerical integration scheme for Hamiltonian systems. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations. They are widely used in nonlinear dynamics, molecular dynamics, discrete element methods, accelerator physics, plasma physics, quantum physics, and celestial mechanics.

The Duffing equation, named after Georg Duffing (1861–1944), is a non-linear second-order differential equation used to model certain damped and driven oscillators. The equation is given by

In fluid dynamics, a Stokes wave is a nonlinear and periodic surface wave on an inviscid fluid layer of constant mean depth. This type of modelling has its origins in the mid 19th century when Sir George Stokes – using a perturbation series approach, now known as the Stokes expansion – obtained approximate solutions for nonlinear wave motion.

The Benjamin–Bona–Mahony equation is the partial differential equation
In mathematical physics, the Hunter–Saxton equation
In fluid dynamics, Luke's variational principle is a Lagrangian variational description of the motion of surface waves on a fluid with a free surface, under the action of gravity. This principle is named after J.C. Luke, who published it in 1967. This variational principle is for incompressible and inviscid potential flows, and is used to derive approximate wave models like the mild-slope equation, or using the averaged Lagrangian approach for wave propagation in inhomogeneous media.

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.
In mathematics, the Kardar–Parisi–Zhang (KPZ) equation is a non-linear stochastic partial differential equation, introduced by Mehran Kardar, Giorgio Parisi, and Yi-Cheng Zhang in 1986. It describes the temporal change of a height field with spatial coordinate and time coordinate :
In analytical mechanics and quantum field theory, minimal coupling refers to a coupling between fields which involves only the charge distribution and not higher multipole moments of the charge distribution. This minimal coupling is in contrast to, for example, Pauli coupling, which includes the magnetic moment of an electron directly in the Lagrangian.
The phase-space formulation of quantum mechanics places the position and momentum variables on equal footing in phase space. In contrast, the Schrödinger picture uses the position or momentum representations. The two key features of the phase-space formulation are that the quantum state is described by a quasiprobability distribution and operator multiplication is replaced by a star product.

In continuum mechanics, Whitham's averaged Lagrangian method – or in short Whitham's method – is used to study the Lagrangian dynamics of slowly-varying wave trains in an inhomogeneous (moving) medium. The method is applicable to both linear and non-linear systems. As a direct consequence of the averaging used in the method, wave action is a conserved property of the wave motion. In contrast, the wave energy is not necessarily conserved, due to the exchange of energy with the mean motion. However the total energy, the sum of the energies in the wave motion and the mean motion, will be conserved for a time-invariant Lagrangian. Further, the averaged Lagrangian has a strong relation to the dispersion relation of the system.
In theoretical physics, Hamiltonian field theory is the field-theoretic analogue to classical Hamiltonian mechanics. It is a formalism in classical field theory alongside Lagrangian field theory. It also has applications in quantum field theory.



























