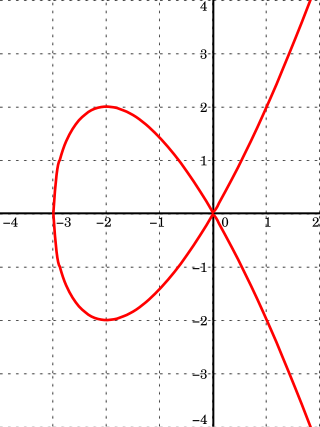In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In geometry, a Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, called coordinate lines, coordinate axes or just axes of the system. The point where the axes meet is called the origin and has (0, 0) as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a Cartesian frame.
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

In computer science, binary space partitioning (BSP) is a method for space partitioning which recursively subdivides a Euclidean space into two convex sets by using hyperplanes as partitions. This process of subdividing gives rise to a representation of objects within the space in the form of a tree data structure known as a BSP tree.
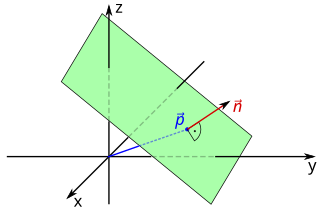
In Euclidean geometry, a plane is a flat two-dimensional surface that extends indefinitely. Euclidean planes often arise as subspaces of three-dimensional space . A prototypical example is one of a room's walls, infinitely extended and assumed infinitesimal thin. While a pair of real numbers suffices to describe points on a plane, the relationship with out-of-plane points requires special consideration for their embedding in the ambient space .

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.

In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcul, are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix. They are also used in fundamental elliptic curve cryptography algorithms.
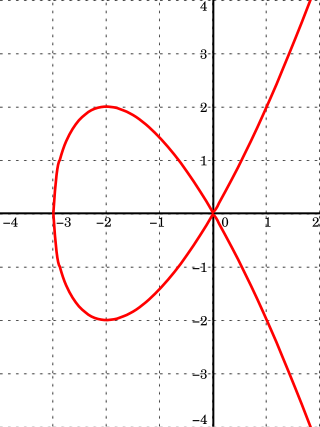
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.

A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.

A vanishing point is a point on the image plane of a perspective rendering where the two-dimensional perspective projections of mutually parallel lines in three-dimensional space appear to converge. When the set of parallel lines is perpendicular to a picture plane, the construction is known as one-point perspective, and their vanishing point corresponds to the oculus, or "eye point", from which the image should be viewed for correct perspective geometry. Traditional linear drawings use objects with one to three sets of parallels, defining one to three vanishing points.

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.
A first-person shooter engine is a video game engine specialized for simulating 3D environments for use in a first-person shooter video game. First-person refers to the view where the players see the world from the eyes of their characters. Shooter refers to games which revolve primarily around wielding firearms and killing other entities in the game world, either non-player characters or other players.

Quake Army Knife (QuArK), is a free and open-source program for developing 3D assets for a large variety of first-person shooters, such as video games using the Quake engine by id Software or the Torque engine.

3D GameStudio or 3DGS is a pan 3D computer game development system which allows the users to create 3D games and other virtual reality applications, and publish them royalty-free. It includes a model/terrain editor, a level editor, a script editor/debugger and comes with a big collection of textures, models and artwork, as well as a game template system that allows the creation of basic shooter games or RPGs without programming. For complex games or other applications, either the integrated programming language named Lite-C or an external development language such as Visual C++ or Borland Delphi can be used.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric.

In geometry, a pole and polar are respectively a point and a line that have a unique reciprocal relationship with respect to a given conic section.
In Euclidean and projective geometry, five points determine a conic, just as two (distinct) points determine a line. There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.

In geometry, an intersection is a point, line, or curve common to two or more objects. The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point or does not exist. Other types of geometric intersection include: