Carry (arithmetic)

Last updated

In elementary arithmetic, a carry is a digit that is transferred from one column of digits to another column of more significant digits. It is part of the standard algorithm to add numbers together by starting with the rightmost digits and working to the left. For example, when 6 and 7 are added to make 13, the "3" is written to the same column and the "1" is carried to the left. When used in subtraction the operation is called a borrow.

Contents

Carrying is emphasized in traditional mathematics, while curricula based on reform mathematics do not emphasize any specific method to find a correct answer.[ citation needed ]

Carrying makes a few appearances in higher mathematics as well. In computing, carrying is an important function of adder circuits.

Manual arithmetic

Example: The addition of two decimal numbers Optellen3.JPG
Example: The addition of two decimal numbers

A typical example of carry is in the following pencil-and-paper addition:

1   27 + 59 ----   86

7 + 9 = 16, and the digit 1 is the carry.

The opposite is a borrow, as in

−1   47 − 19 ----   28

Here, 7 − 9 = −2, so try (10 − 9) + 7 = 8, and the 10 is got by taking ("borrowing") 1 from the next digit to the left. There are two ways in which this is commonly taught:

  1. The ten is moved from the next digit left, leaving in this example 3 − 1 in the tens column. According to this method, the term "borrow" is a misnomer, since the ten is never paid back.
  2. The ten is copied from the next digit left, and then 'paid back' by adding it to the subtrahend in the column from which it was 'borrowed', giving in this example 4 − (1 + 1) in the tens column.

Mathematics education

Traditionally, carry is taught in the addition of multi-digit numbers in the 2nd or late first year of elementary school. However, since the late 20th century, many widely adopted curricula developed in the United States such as TERC omitted instruction of the traditional carry method in favor of invented arithmetic methods, and methods using coloring, manipulatives, and charts. Such omissions were criticized by such groups as Mathematically Correct, and some states and districts have since abandoned this experiment, though it remains widely used.[ citation needed ]

Higher mathematics

Kummer's theorem states that the number of carries involved in adding two numbers in base is equal to the exponent of the highest power of dividing a certain binomial coefficient.

When several random numbers of many digits are added, the statistics of the carry digits bears an unexpected connection with Eulerian numbers and the statistics of riffle shuffle permutations. [1] [2] [3] [4]

In abstract algebra, the carry operation for two-digit numbers can be formalized using the language of group cohomology. [5] [6] [7] This viewpoint can be applied to alternative characterizations of the real numbers. [8] [9]

Mechanical calculators

Carry represents one of the basic challenges facing designers and builders of mechanical calculators. They face two basic difficulties: The first one stems from the fact that a carry can require several digits to change: in order to add 1 to 999, the machine has to increment 4 different digits. Another challenge is the fact that the carry can "develop" before the next digit finished the addition operation.

Most mechanical calculators implement carry by executing a separate carry cycle after the addition itself. During the addition, each carry is "signaled" rather than performed, and during the carry cycle, the machine increments the digits above the "triggered" digits. This operation has to be performed sequentially, starting with the ones digit, then the tens, the hundreds, and so on, since adding the carry can generate a new carry in the next digit.

Some machines, notably Pascal's calculator, the second known calculator to be built, and the oldest surviving, use a different method: incrementing the digit from 0 to 9, cocks a mechanical device to store energy, and the next increment, which moves the digit from 9 to 0, releases this energy to increment the next digit by 1. Pascal used weights and gravity in his machine. Another notable machine using similar method is the highly successful 19th century Comptometer, which replaced the weights with springs.

Some innovative machines use continuous transmission: adding 1 to any digit, advances the next one by 1/10 (which in turn advances the next one by 1/100 and so on). Some innovative early calculators, notably Chebyshev calculator from 1870, [10] and a design by Selling, [11] from 1886, used this method, but neither were successful. In the early 1930, Marchant calculator implemented continuous transmission with great success, starting with the aptly named "Silent Speed" calculator. Marchant (later to become SCM Corporation) continued to use and improve it, and made continuous-transmission calculators with unmatched speed, into the late 1960s, to the end of the mechanical calculator era.

Computing

When speaking of a digital circuit like an adder, the word carry is used in a similar sense.

In most computers, the carry from the most significant bit of an arithmetic operation (or bit shifted out from a shift operation) is placed in a special carry bit which can be used as a carry-in for multiple precision arithmetic or tested and used to control execution of a computer program. The same carry bit is also generally used to indicate borrows in subtraction, though the bit's meaning is inverted due to the effects of two's complement arithmetic. Normally, a carry bit value of "1" signifies that an addition overflowed the ALU, and must be accounted for when adding data words of lengths greater than that of the CPU. For subtractive operations, two (opposite) conventions are employed as most machines set the carry flag on borrow while some machines (such as the 6502 and the PIC) instead reset the carry flag on borrow (and vice versa).

Related Research Articles

<span class="mw-page-title-main">Arithmetic</span> Elementary branch of mathematics

Arithmetic is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers—addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today.

<span class="mw-page-title-main">Binary-coded decimal</span> System of digitally encoding numbers

In computing and an electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used for a sign or other indications.

<span class="mw-page-title-main">Difference engine</span> Automatic mechanical calculator designed to tabulate polynomial functions

A difference engine is an automatic mechanical calculator designed to tabulate polynomial functions. It was designed in the 1820s, and was first created by Charles Babbage. The name, the difference engine, is derived from the method of divided differences, a way to interpolate or tabulate functions by using a small set of polynomial co-efficients. Some of the most common mathematical functions used in engineering, science and navigation, were, and still are computable with the use of the difference engine's capability of computing logarithmic and trigonometric functions, which can be approximated by polynomials, so a difference engine can compute many useful tables of numbers.

<span class="mw-page-title-main">Floating-point arithmetic</span> Computer approximation for real numbers

In computing, floating-point arithmetic (FP) is arithmetic using formulaic representation of real numbers as an approximation to support a trade-off between range and precision. For this reason, floating-point computation is often used in systems with very small and very large real numbers that require fast processing times. In general, a floating-point number is represented approximately with a fixed number of significant digits and scaled using an exponent in some fixed base; the base for the scaling is normally two, ten, or sixteen. A number that can be represented exactly is of the following form:

<span class="mw-page-title-main">Multiplication table</span> Mathematical table

In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system.

A multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are used. Efficient multiplication algorithms have existed since the advent of the decimal system.

<span class="mw-page-title-main">Addition</span> Arithmetic operation

Addition is one of the four basic operations of arithmetic, the other three being subtraction, multiplication and division. The addition of two whole numbers results in the total amount or sum of those values combined. The example in the adjacent image shows a combination of three apples and two apples, making a total of five apples. This observation is equivalent to the mathematical expression "3 + 2 = 5".

<span class="mw-page-title-main">Subtraction</span> One of the four basic arithmetic operations

Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, −. For example, in the adjacent picture, there are 5 − 2 peaches—meaning 5 peaches with 2 taken away, resulting in a total of 3 peaches. Therefore, the difference of 5 and 2 is 3; that is, 5 − 2 = 3. While primarily associated with natural numbers in arithmetic, subtraction can also represent removing or decreasing physical and abstract quantities using different kinds of objects including negative numbers, fractions, irrational numbers, vectors, decimals, functions, and matrices.

A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method of mathematical expression which uses only two symbols: typically "0" (zero) and "1" (one).

Two's complement is a mathematical operation to reversibly convert a positive binary number into a negative binary number with equivalent value, using the binary digit with the greatest place value to indicate whether the binary number is positive or negative. It is used in computer science as the most common method of representing signed integers on computers, and more generally, fixed point binary values. When the most significant bit is a one, the number is signed as negative. (see Converting from two's complement representation, below).

Method of complements Method of subtraction

In mathematics and computing, the method of complements is a technique to encode a symmetric range of positive and negative integers in a way that they can use the same algorithm (hardware) for addition throughout the whole range. For a given number of places half of the possible representations of numbers encode the positive numbers, the other half represents their respective additive inverses. The pairs of mutually additive inverse numbers are called complements. Thus subtraction of any number is implemented by adding its complement. Changing the sign of any number is encoded by generating its complement, which can be done by a very simple and efficient algorithm. This method was commonly used in mechanical calculators and is still used in modern computers. The generalized concept of the radix complement is also valuable in number theory, such as in Midy's theorem.

Mechanical calculator Mechanical machine for arithmetic operations for absolute calculators

A mechanical calculator, or calculating machine, is a mechanical device used to perform the basic operations of arithmetic automatically, or (historically) a simulation such as an analog computer or a slide rule. Most mechanical calculators were comparable in size to small desktop computers and have been rendered obsolete by the advent of the electronic calculator and the digital computer.

The Trachtenberg system is a system of rapid mental calculation. The system consists of a number of readily memorized operations that allow one to perform arithmetic computations very quickly. It was developed by the Russian engineer Jakow Trachtenberg in order to keep his mind occupied while being in a Nazi concentration camp.

In computer science, arbitrary-precision arithmetic, also called bignum arithmetic, multiple-precision arithmetic, or sometimes infinite-precision arithmetic, indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most arithmetic logic unit (ALU) hardware, which typically offers between 8 and 64 bits of precision.

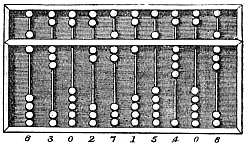
<span class="mw-page-title-main">Suanpan</span> Chinese abacus

The suanpan, also spelled suan pan or souanpan) is an abacus of Chinese origin first described in a 190 CE book of the Eastern Han Dynasty, namely Supplementary Notes on the Art of Figures written by Xu Yue. However, the exact design of this suanpan is not known. Usually, a suanpan is about 20 cm (8 in) tall and it comes in various widths depending on the application. It usually has more than seven rods. There are two beads on each rod in the upper deck and five beads on each rod in the bottom deck. The beads are usually rounded and made of a hardwood. The beads are counted by moving them up or down towards the beam. The suanpan can be reset to the starting position instantly by a quick jerk around the horizontal axis to spin all the beads away from the horizontal beam at the center.

<span class="mw-page-title-main">Elementary arithmetic</span> Numbers and the basic operations on them

In arithmetic, the elementary operations are addition, subtraction, multiplication, and division. Elementary arithmetic also includes operations on fractions and negative numbers, which can be represented on a number line.

<span class="mw-page-title-main">Pascal's calculator</span> Early mechanical calculator

Pascal's calculator is a mechanical calculator invented by Blaise Pascal in 1642. Pascal was led to develop a calculator by the laborious arithmetical calculations required by his father's work as the supervisor of taxes in Rouen. He designed the machine to add and subtract two numbers directly and to perform multiplication and division through repeated addition or subtraction.

<span class="mw-page-title-main">Integer overflow</span> When representing an arithmetic result requires more digits than are available

In computer programming, an integer overflow occurs when an arithmetic operation attempts to create a numeric value that is outside of the range that can be represented with a given number of digits – either higher than the maximum or lower than the minimum representable value.

Decimal floating-point (DFP) arithmetic refers to both a representation and operations on decimal floating-point numbers. Working directly with decimal (base-10) fractions can avoid the rounding errors that otherwise typically occur when converting between decimal fractions and binary (base-2) fractions.

Arithmetic logic unit Combinational digital circuit

In computing, an arithmetic logic unit (ALU) is a combinational digital circuit that performs arithmetic and bitwise operations on integer binary numbers. This is in contrast to a floating-point unit (FPU), which operates on floating point numbers. It is a fundamental building block of many types of computing circuits, including the central processing unit (CPU) of computers, FPUs, and graphics processing units (GPUs).

References

  1. ↑ Holte, John M. (February 1997), "Carries, Combinatorics, and an Amazing Matrix", The American Mathematical Monthly, 104 (2): 138–149, doi:10.2307/2974981, JSTOR   2974981
  2. ↑ Diaconis, Persi; Fulman, Jason (August 2009), "Carries, shuffling, and symmetric functions", Advances in Applied Mathematics, 43 (2): 176–196, arXiv: 0902.0179 , doi:10.1016/j.aam.2009.02.002
  3. ↑ Borodin, Alexei; Diaconis, Persi; Fulman, Jason (October 2010), "On adding a list of numbers (and other one-dependent determinantal processes)", Bulletin of the American Mathematical Society, 47 (4): 639–670, arXiv: 0904.3740 , doi:10.1090/S0273-0979-2010-01306-9
  4. ↑ Nakano, Fumihiko; Sadahiro, Taizo (February 2014), "A generalization of carries processes and Eulerian numbers", Advances in Applied Mathematics, 53: 28–43, doi: 10.1016/j.aam.2013.09.005
  5. ↑ Hegland, M.; Wheeler, W. W. (January 1997), "Linear Bijections and the Fast Fourier Transform", Applicable Algebra in Engineering, Communication and Computing, 8 (2): 143–163, doi:10.1007/s002000050059
  6. ↑ Isaksen, Daniel C. (November 2002), "A Cohomological Viewpoint on Elementary School Arithmetic" (PDF), The American Mathematical Monthly, 109 (9): 796–805, doi:10.2307/3072368, JSTOR   3072368, archived from the original (PDF) on January 16, 2014, retrieved January 22, 2014
  7. ↑ Borovik, Alexandre V. (2010), Mathematics under the Microscope: Notes on Cognitive Aspects of Mathematical Practice, AMS, pp. 87–88, ISBN   978-0-8218-4761-9
  8. ↑ Metropolis, N.; Gian-Carlo, Rota; Tanny, S. (May 1973), "Significance Arithmetic: The Carrying Algorithm", Journal of Combinatorial Theory, Series A , 14 (3): 386–421, doi: 10.1016/0097-3165(73)90013-7
  9. ↑ Faltin, F.; Metropolis, N.; Ross, B.; Rota, G.-C. (June 1975), "The Real Numbers as a Wreath Product", Advances in Mathematics , 16 (3): 278–304, doi: 10.1016/0001-8708(75)90115-2
  10. ↑ Roegel, Denis (2015). "Chebyshev's continuous adding machine" (PDF). Archived (PDF) from the original on 2017-08-09.
  11. ↑ Ernst, Martin (1925). The Calculating Machines (PDF). Charles Babbage Institute. p. 96.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.