Centipede mathematics is a term used, sometimes derogatorily, [1] to describe the generalization and study of mathematical objects satisfying progressively fewer and fewer restrictions. This type of study is likened to studying how a centipede behaves when its legs are removed one by one.
The term is attributed to Polish mathematician Antoni Zygmund. Zygmund is said to have described the metaphor of the centipede thus: "You take a centipede and pull off ninety-nine of its legs and see what it can do." [2] Thus, Zygmund has been known by many mathematicians as the "Centipede Surgeon".
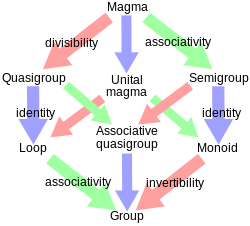
The study of semigroups is cited as an example of doing centipede mathematics. [3] One starts with the notion of an abelian group. First delete the commutativity restriction to obtain the concept of a group. The restriction of existence of inverses is then removed. This produces a monoid. If one now removes the restriction regarding the existence of identity, the resulting object turns out to be a semigroup. Still more legs can be removed. If the associativity restriction is also discarded one gets a magma or a groupoid. The restrictions that define an abelian group may be removed in different orders also. The study of ternary ring has been cited as an example of centipede mathematics. The progressive removal of axioms of Euclidean geometry and studying the resulting geometrical objects also illustrate the methodology of centipede mathematics. [4]
The following quote summarises the value and usefulness of the concept: "The term ‘centipede mathematics’ is new to me, but its practice is surely of great antiquity. The binomial theorem (tear off the leg that says that the exponent has to be a natural number) is a good example. A related notion is the importance of good notation and the importance of overloading, aka abuse of language, to establish useful analogies." — Gavin Wraith. [3]