
In mathematics, an exponential function is a function of the form
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures, through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.
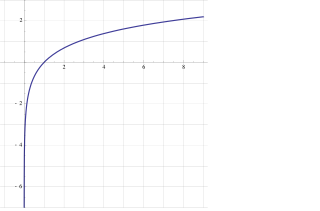
The natural logarithm of a number is its logarithm to the base of the mathematical constant e, where e is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x) or log(x). This is done in particular when the argument to the logarithm is not a single symbol, to prevent ambiguity.
The number π is a mathematical constant. Originally defined as the ratio of a circle's circumference to its diameter, it now has various equivalent definitions and appears in many formulas in all areas of mathematics and physics. It is approximately equal to 3.14159. It has been represented by the Greek letter "π" since the mid-18th century, though it is also sometimes spelled out as "pi". It is also called Archimedes' constant.
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction, the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers are called the coefficients or terms of the continued fraction.
In mathematics, a power series is an infinite series of the form
In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series is said to converge absolutely if for some real number . Similarly, an improper integral of a function, , is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if
In mathematics, a quadratic equation is a polynomial equation of the second degree. The general form is
In the analytic theory of continued fractions, Euler's continued fraction formula is an identity connecting a certain very general infinite series with an infinite continued fraction. First published in 1748, it was at first regarded as a simple identity connecting a finite sum with a finite continued fraction in such a way that the extension to the infinite case was immediately apparent. Today it is more fully appreciated as a useful tool in analytic attacks on the general convergence problem for infinite continued fractions with complex elements.
Stochastic approximation algorithms are recursive update rules that can be used, among other things, to solve optimization problems and fixed point equations when the collected data is subject to noise. In engineering, optimization problems are often of this type when you do not have a mathematical model of the system but still would like to optimize its behavior by adjusting certain parameters.
In mathematics, an infinite periodic continued fraction is a continued fraction that can be placed in the form

In complex analysis, a Padé table is an array, possibly of infinite extent, of the rational Padé approximants
In complex analysis, Gauss's continued fraction is a particular class of continued fractions derived from hypergeometric functions. It was one of the first analytic continued fractions known to mathematics, and it can be used to represent several important elementary functions, as well as some of the more complicated transcendental functions.
The square root of 5 is the positive real number that, when multiplied by itself, gives the prime number 5. It is more precisely called the principal square root of 5, to distinguish it from the negative number with the same property. This number appears in the fractional expression for the golden ratio. It can be denoted in surd form as:
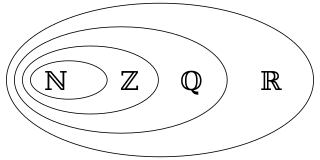
In mathematics, a rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Since q may be equal to 1, every integer is a rational number. The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q ; it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient".
In mathematics, for a sequence of complex numbers a1, a2, a3, ... the infinite product
In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. Some functions can actually be expanded directly as infinite compositions. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. For infinite compositions of a single function see Iterated function. For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.
Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.








