
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).

In geometry, rhombicuboctahedron is an Archimedean solid with 26 faces, consisting of 8 equilateral triangles and 18 squares. It is named by Johannes Kepler in his 1618 Harmonices Mundi, being short for truncated cuboctahedral rhombus, with cuboctahedral rhombus being his name for a rhombic dodecahedron.
9 (nine) is the natural number following 8 and preceding 10.
8 (eight) is the natural number following 7 and preceding 9.

Elamkulam Manakkal Sankaran Namboodiripad, popularly known as 'E.M.S. Namboodiripad' or simply by his initials 'E. M. S.', was an Indian communist politician and theorist, who served as the first Chief Minister of Kerala in 1957–1959 and then again in 1967–1969. As a member of the Communist Party of India (CPI), he became the first non-Congress Chief Minister in the Indian republic. In 1964, he led a faction of the CPI that broke away to form the Communist Party of India (Marxist).

Mathematics and architecture are related, since, as with other arts, architects use mathematics for several reasons. Apart from the mathematics needed when engineering buildings, architects use geometry: to define the spatial form of a building; from the Pythagoreans of the sixth century BC onwards, to create forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, aesthetic and sometimes religious principles; to decorate buildings with mathematical objects such as tessellations; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings.

In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.
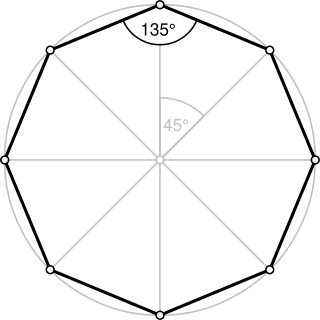
In geometry, an octagon is an eight-sided polygon or 8-gon.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

In mathematics, two quantities are in the silver ratio if the ratio of the larger of those two quantities to the smaller quantity is the same as the ratio of the sum of the smaller quantity plus twice the larger quantity to the larger quantity. This defines the silver ratio as an irrational mathematical constant, whose value of one plus the square root of 2 is approximately 2.4142135623. Its name is an allusion to the golden ratio; analogously to the way the golden ratio is the limiting ratio of consecutive Fibonacci numbers, the silver ratio is the limiting ratio of consecutive Pell numbers. The silver ratio is sometimes denoted by δS but it can vary from λ to σ.

In geometry, the square cupola is the cupola with octagonal base. In the case of edges are equal in length, it is the Johnson solid, a convex polyhedron with faces are regular. It can be used to construct many polyhedrons, particularly in other Johnson solids.

In geometry, the elongated square cupola is a polyhedron constructed from an octagonal prism by attaching square cupola onto its base. It is an example of Johnson solid.

In geometry, the elongated square gyrobicupola is a polyhedron constructed by two square cupolas attaching onto the bases of octagonal prism, with one of them rotated. It was once mistakenly considered a rhombicuboctahedron by many mathematicians. It is not considered to be an Archimedean solid because it lacks a set of global symmetries that map every vertex to every other vertex, unlike the 13 Archimedean solids. It is also a canonical polyhedron. For this reason, it is also known as pseudo-rhombicuboctahedron, Miller solid, or Miller–Askinuze solid.

In geometry, the gyroelongated square bicupola is the Johnson solid constructed by attaching two square cupolae on each base of octagonal antiprism. It has the property of chirality.
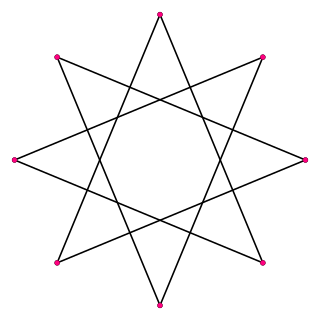
In geometry, an octagram is an eight-angled star polygon.

In mathematics, a hexadecagon is a sixteen-sided polygon.

Egyptian geometry refers to geometry as it was developed and used in Ancient Egypt. Their geometry was a necessary outgrowth of surveying to preserve the layout and ownership of farmland, which was flooded annually by the Nile river.

A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.
Kanippayyur Shankaran Namboodiripad (1891-1981) was a Nambudiri Brahmin in the State of Kerala in India who helped rejuvenate interest in the Indian traditional architectural styles known collectively as Vastu shastra. He was a consultant for the renovation of many temples in Kerala, Tamil Nadu and Karnataka, and also the Royal Architect for the three royal families of Travancore, Cochin and Kozhikode (Calicut). He was a prolific writer authoring more than a hundred books on a variety of books relating to traditional knowledge areas like vastu shastra (architecture), jyothisha, ayurveda, and also books on history. He compiled a Sanskrit-Malayalam Dictionary and a Dictionary of Indigenous Medicines.
Allakuri Mosque, located in the Mohammadpur Colony area near Sat Masjid Road of Dhaka, is an example of the imperial Mughal architecture in Bangladesh. The mosque was tentatively built in 1680 and is the earliest known square single-domed Mughal style mosque in Bengal.















