Chinese multiplication table

Last updated August 27, 2024

The Chinese multiplication table is the first requisite for using the Rod calculus for carrying out multiplication, division, the extraction of square roots, and the solving of equations based on place value decimal notation. It was known in China as early as the Spring and Autumn period, and survived through the age of the abacus; pupils in elementary school today still must memorise it.^[1]

The Chinese multiplication table consists of eighty-one terms. It was often called the nine-nine table, or simply nine-nine, because in ancient times, the nine nine table started with 9 × 9:^[2] nine nines beget eighty-one, eight nines beget seventy-two ... seven nines beget sixty three, etc. two ones beget two. In the opinion of Wang Guowei, a noted scholar, the nine-nine table probably started with nine because of the "worship of nine" in ancient China; the emperor was considered the "nine five supremacy" in the Book of Change. See also Numbers in Chinese culture § Nine.

It is also known as nine-nine song (or poem),^[2] as the table consists of eighty-one lines with four or five Chinese characters per lines; this thus created a constant metre and render the multiplication table as a poem. For example, 9 × 9 = 81 would be rendered as "九九八十一", or "nine nine eighty one", with the world for "begets" "得" implied. This makes it easy to learn by heart.^[1] A shorter version of the table consists of only forty-five sentences, as terms such as "nine eights beget seventy-two" are identical to "eight nines beget seventy-two" so there is no need to learn them twice. When the abacus replaced the counting rods in the Ming dynasty, many authors^{[ who? ]} on the abacus advocated the use of the full table instead of the shorter one. They claimed that memorising it without needing ag a moment of thinking makes abacus calculation much faster.^{[ citation needed ]}

The existence of the Chinese multiplication table is evidence of an early positional decimal system: otherwise a much larger multiplication table would be needed with terms beyond 9×9.

The Nine-nine song text in Chinese

It can be read in either row-major or column-major order.

九九乘法口诀表 (The Nine-nine multiplication table)
	1 一 yī	2 二 èr	3 三 sān	4 四 sì	5 五 wǔ	6 六 liù	7 七 qī	8 八 bā	9 九 jiǔ
1 一 yī	一一得一
2 二 èr	一二得二	二二得四
3 三 sān	一三得三	二三得六	三三得九
4 四 sì	一四得四	二四得八	三四十二	四四十六
5 五 wǔ	一五得五	二五一十	三五十五	四五二十	五五二十五
6 六 liù	一六得六	二六十二	三六十八	四六二十四	五六三十	六六三十六
7 七 qī	一七得七	二七十四	三七二十一	四七二十八	五七三十五	六七四十二	七七四十九
8 八 bā	一八得八	二八十六	三八二十四	四八三十二	五八四十	六八四十八	七八五十六	八八六十四
9 九 jiǔ	一九得九	二九十八	三九二十七	四九三十六	五九四十五	六九五十四	七九六十三	八九七十二	九九八十一

Nine-nine multiplication table
	1 One yī	2 Two èr	3 Three sān	4 Four sì	5 Five wǔ	6 Six liù	7 Seven qī	8 Eight bā	9 Nine jiǔ
1 One yī	One times one equals one
2 Two èr	One times two equals two	Two times two equals four
3 Three sān	One times three equals three	Two times three equals six	Three times three equals nine
4 Four sì	One times four equals four	Two times four equals eight	Three times four equals twelve	Four times four equals sixteen
5 Five wǔ	One times five equals five	Two times five equals ten	Three times five equals fifteen	Four times five equals twenty	Five times five equals twenty-five
6 Six liù	One times six equals six	Two times six equals twelve	Three times six equals eighteen	Four times six equals twenty-four	Five times six equals thirty	Six times six equals thirty-six
7 Seven qī	One times seven equals seven	Two times seven equals fourteen	Three times seven equals twenty-one	Four times seven equals twenty-eight	Five times seven equals thirty-five	Six times seven equals forty-two	Seven times seven equals forty-nine
8 Eight bā	One times eight equals eight	Two times eight equals sixteen	Three times eight equals twenty-four	Four times eight equals thirty-two	Five times eight equals forty	Six times eight equals forty-eight	Seven times eight equals fifty-six	Eight times eight equals sixty-four
9 Nine jiǔ	One times nine equals nine	Two times nine equals eighteen	Three times nine equals twenty-seven	Four times nine equals thirty-six	Five times nine equals forty-five	Six times nine equals fifty-four	Seven times nine equals sixty-three	Eight times nine equals seventy-two	Nine times nine equals eighty-one

The Nine-nine table in Chinese literature

Many Chinese classics make reference to the nine-nine table:

Zhoubi Suanjing: "nine nine eighty one"
Guan Zi has sentences of the form "three eights beget twenty four, three sevens beget twenty-one"
The Nine Chapters on the Mathematical Art: "Fu Xi invented the art of nine-nine".
In Huainanzi, there were eight sentences: "nine nines beget eighty one", "eight nines beget seventy two", all the way to "two nines beget eighteen".
A nine-nine table manuscript was discovered in Dun Huang.^[2]
Xia Houyang's Computational Canons: "To learn the art of multiplication and division, one must understand nine-nine".
The Song dynasty author Hong Zhai's Notebooks said: "three threes as nine, three fours as twelve, two eights as sixteen, four fours as sixteen, three nines as twenty seven, four nines as thirty six, six sixes as thirty six, five eights as forty, five nines as forty five, seven nines as sixty three, eight nines as seventy two, nine nines as eighty one". This suggests that the table has begun with the smallest term since the Song dynasty.
Song dynasty mathematician Yang Hui's mathematics text book: Suan fa tong bian ben mo, meaning "You must learn nine nine song from one one equals one to nine nine eighty one, in small to large order"
Yuan dynasty mathematician Zhu Shijie's Suanxue qimeng (Elementary mathematics): "one one equals one, two by two equals four, one by three equals three, two by three equals six, three by three equals nine, one by four equals four... nine by nine equals eight one"

Archeological artifacts

At the end of the 19th century, archeologists unearthed pieces of written bamboo script from the Han dynasty in Xin Jiang. One such Han dynasty bamboo script, from Liusha, is a remnant of the nine-nine table. It starts with nine: nine nine eighty one, eight nine seventy two, seven nine sixty three, eight eight sixty four, seven eight fifty six, six eight forty eight, ... two two gets four, altogether 1100 Chinese words.
In 2002, Chinese archeologists unearthed a written wood script from a two-thousand-year-old site from the Warring States, on which was written: "four eight thirty two, five eight forty, six eight forty eight." This is the earliest artifact of the nine-nine table that has been unearthed, indicating that the nine-nine table, as well as a positional decimal system, had appeared by the Warring States period.
Tsinghua Bamboo Slips Calculation Table, is an ancient calculator artifact from the Warring States period in 305 BC. It is included in the "Tsinghua University Collection of Warring States Bamboo Slips (Part IV)," predating the previously discovered Liye Qin Bamboo Slips and Zhangjiashan Han Bamboo Slips nine-nine tables by a century.
In 2023, a bamboo slip from the 4th century BC, containing a multiplication formula, was found in a Jingzhou tomb in Hubei Province, China. The formula was deciphered using infrared scanning, revealing calculations such as "five times seven is thirty plus five, four times seven is twenty plus eight, three times seven is twenty plus one." As of December 2023, this represents the earliest discovery of a nine-nine table artifact.
The nine-nine table was transmitted to Japan, and appeared in a Japanese primary mathematics book in the 10th century, beginning with 9×9.

Related Research Articles

An abacus, also called a counting frame, is a hand-operated calculating tool which was used from ancient times in the ancient Near East, Europe, China, and Russia, until the adoption of the Arabic numeral system. An abacus consists of a two-dimensional array of slidable beads. In their earliest designs, the beads could be loose on a flat surface or sliding in grooves. Later the beads were made to slide on rods and built into a frame, allowing faster manipulation.

In linguistics, a numeral in the broadest sense is a word or phrase that describes a numerical quantity. Some theories of grammar use the word "numeral" to refer to cardinal numbers that act as a determiner that specify the quantity of a noun, for example the "two" in "two hats". Some theories of grammar do not include determiners as a part of speech and consider "two" in this example to be an adjective. Some theories consider "numeral" to be a synonym for "number" and assign all numbers to a part of speech called "numerals". Numerals in the broad sense can also be analyzed as a noun, as a pronoun, or for a small number of words as an adverb.

Tien Gow or Tin Kau is the name of Chinese gambling games played with either a pair of dice or a set of 32 Chinese dominoes. In these games, Heaven is the top rank of the civil suit, while Nine is the top rank of the military suit. The civil suit was originally called the Chinese (華) suit while the military suit was called the barbarian (夷) suit but this was changed during the Qing dynasty to avoid offending the ruling Manchus. The highly idiosyncratic and culture-specific suit-system of these games is likely the conceptual origin of suits, an idea that later is used for playing cards. Play is counter-clockwise.

In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system.

Sugarloaf Township is a township in Columbia County, Pennsylvania. It is part of Northeastern Pennsylvania.

English number words include numerals and various words derived from them, as well as a large number of words borrowed from other languages.

<span class="mw-page-title-main">Vigesimal</span> Base-20 numeral system

A vigesimal or base-20 (base-score) numeral system is based on twenty. Vigesimal is derived from the Latin adjective vicesimus, meaning 'twentieth'.

Napier's bones is a manually-operated calculating device created by John Napier of Merchiston, Scotland for the calculation of products and quotients of numbers. The method was based on lattice multiplication, and also called rabdology, a word invented by Napier. Napier published his version in 1617. It was printed in Edinburgh and dedicated to his patron Alexander Seton.

-yllion is a proposal from Donald Knuth for the terminology and symbols of an alternate decimal superbase system. In it, he adapts the familiar English terms for large numbers to provide a systematic set of names for much larger numbers. In addition to providing an extended range, -yllion also dodges the long and short scale ambiguity of -illion.

Positional notation usually denotes the extension to any base of the Hindu–Arabic numeral system. More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred. In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string.

The soroban is an abacus developed in Japan. It is derived from the ancient Chinese suanpan, imported to Japan in the 14th century. Like the suanpan, the soroban is still used today, despite the proliferation of practical and affordable pocket electronic calculators.

An autogram is a sentence that describes itself in the sense of providing an inventory of its own characters. They were invented by Lee Sallows, who also coined the word autogram. An essential feature is the use of full cardinal number names such as "one", "two", etc., in recording character counts. Autograms are also called 'self-enumerating' or 'self-documenting' sentences. Often, letter counts only are recorded while punctuation signs are ignored, as in this example:

This sentence employs two a's, two c's, two d's, twenty-eight e's, five f's, three g's, eight h's, eleven i's, three l's, two m's, thirteen n's, nine o's, two p's, five r's, twenty-five s's, twenty-three t's, six v's, ten w's, two x's, five y's, and one z.

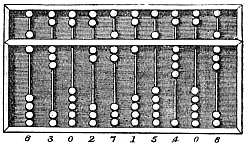
<span class="mw-page-title-main">Suanpan</span> Chinese abacus

The suanpan, also spelled suan pan or souanpan) is an abacus of Chinese origin, earliest first known written documentation of the Chinese abacus dates to the 2nd century BCE during the Han dynasty, and later, described in a 190 CE book of the Eastern Han dynasty, namely Supplementary Notes on the Art of Figures written by Xu Yue. However, the exact design of this suanpan is not known. Usually, a suanpan is about 20 cm (8 in) tall and it comes in various widths depending on the application. It usually has more than seven rods. There are two beads on each rod in the upper deck and five beads on each rod in the bottom deck. The beads are usually rounded and made of a hardwood. The beads are counted by moving them up or down towards the beam. The suanpan can be reset to the starting position instantly by a quick jerk around the horizontal axis to spin all the beads away from the horizontal beam at the center.

Mathematics emerged independently in China by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system, algebra, geometry, number theory and trigonometry.

Xiàzhì is the 10th solar term, and marks the summer solstice, in the traditional Chinese lunisolar calendar dividing a year into 24 solar terms.

145th Street is a major crosstown street in the Harlem neighborhood, in the New York City borough of Manhattan. It is one of the 15 crosstown streets mapped out in the Commissioner's Plan of 1811 that established the numbered street grid in Manhattan. It forms the southern border of the Sugar Hill neighborhood within Harlem.

Miship, or Chip, is an Afro-Asiatic language spoken in Plateau State, Nigeria. Doka is a dialect. Blench lists the two dialects Longmaar and Jiɓaam.

Counting rods (筭) are small bars, typically 3–14 cm long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number.

The Battle of Tonkin River was a major naval battle fought in northern Vietnam between the pirates of Shap Ng-tsai and the British Royal Navy with aid from the Qing Chinese navy and the Tonkinese. The 1849 expedition led to the destruction of Shap Ng-tsai's fleet and the loss of over 2,000 men. The battle occurred over a three-day period at the mouth of the Tonkin River, near present-day Hai Phong.

<span class="mw-page-title-main">Liye Qin Slips</span>

The Liye Qin Slips is a large collection of bamboo slips which were unearthed from Liye Ancient City in Longshan County, Hunan, China in 2002. It is one of China's most important archaeological discoveries of the 21st century. Archaeologists found more than 37,000 pieces of bamboo slips, on which more than 200,000 Chinese characters record government and legal documents of the Qin dynasty. It is considered the most important archaeological discovery of the Qin dynasty after the Terracotta Army unearthed in 1973 in Xi'an.

References

1 2 Prado, Jerome; Lu, Jiayan; Dong, Xi; Zhou, Xinlin; Booth, James R (May 2013). "The neural bases of the multiplication problem-size effect across countries". Frontiers in Human Neuroscience. 7: 52. doi: 10.3389/fnhum.2013.00189 . ISBN 9782889198160. PMC 3651960 . PMID 23717274 . Retrieved 12 April 2019.
1 2 3 Lam Lay Yong; Ang Tian Se (2004). Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in ancient China. World Scientific. pp. 73–77. ISBN 9789814483605.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[FHN13-1] 1 2 Prado, Jerome; Lu, Jiayan; Dong, Xi; Zhou, Xinlin; Booth, James R (May 2013). "The neural bases of the multiplication problem-size effect across countries". Frontiers in Human Neuroscience. 7: 52. doi: 10.3389/fnhum.2013.00189 . ISBN 9782889198160. PMC 3651960 . PMID 23717274 . Retrieved 12 April 2019.

[TCAA-2] 1 2 3 Lam Lay Yong; Ang Tian Se (2004). Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in ancient China. World Scientific. pp. 73–77. ISBN 9789814483605.

[1]

[2]