Definition
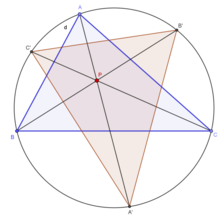
Let P be a point in the plane of the reference triangle △ABC. Let the lines AP, BP, CP intersect the circumcircle of △ABC at A', B', C'. The triangle △A'B'C' is called the circumcevian triangle of P with reference to △ABC. [1]
In Euclidean geometry, a circumcevian triangle is a special triangle associated with a reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle.

Let P be a point in the plane of the reference triangle △ABC. Let the lines AP, BP, CP intersect the circumcircle of △ABC at A', B', C'. The triangle △A'B'C' is called the circumcevian triangle of P with reference to △ABC. [1]
Let a,b,c be the side lengths of triangle △ABC and let the trilinear coordinates of P be α : β : γ. Then the trilinear coordinates of the vertices of the circumcevian triangle of P are as follows: [2]
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
In geometry, Heron's formula gives the area of a triangle in terms of the three side lengths a, b, c. If is the semiperimeter of the triangle, the area A is,

In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex. The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex.

In plane geometry, Morley's trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the first Morley triangle or simply the Morley triangle. The theorem was discovered in 1899 by Anglo-American mathematician Frank Morley. It has various generalizations; in particular, if all the trisectors are intersected, one obtains four other equilateral triangles.
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.
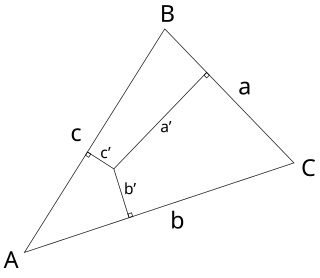
In geometry, the trilinear coordinatesx : y : z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x : y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y : z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z : x and vertices C and A.

In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician.
In geometry, calculating the area of a triangle is an elementary problem encountered often in many different situations. The best known and simplest formula is where b is the length of the base of the triangle, and h is the height or altitude of the triangle. The term "base" denotes any side, and "height" denotes the length of a perpendicular from the vertex opposite the base onto the line containing the base. Euclid proved that the area of a triangle is half that of a parallelogram with the same base and height in his book Elements in 300 BCE. In 499 CE Aryabhata, used this illustrated method in the Aryabhatiya.
In Euclidean geometry, a circumconic is a conic section that passes through the three vertices of a triangle, and an inconic is a conic section inscribed in the sides, possibly extended, of a triangle.

In geometry, a triangle center or triangle centre is a point in the triangle's plane that is in some sense in the middle of the triangle. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:
Solution of triangles is the main trigonometric problem of finding the characteristics of a triangle, when some of these are known. The triangle can be located on a plane or on a sphere. Applications requiring triangle solutions include geodesy, astronomy, construction, and navigation.
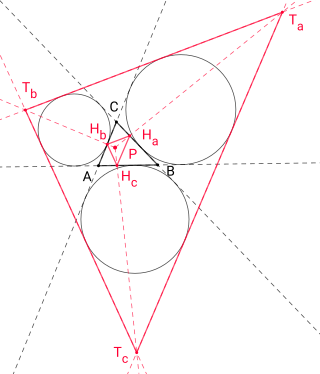
The Clawson point is a special point in a planar triangle defined by the trilinear coordinates , where are the interior angles at the triangle vertices . It is named after John Wentworth Clawson, who published it 1925 in the American Mathematical Monthly.
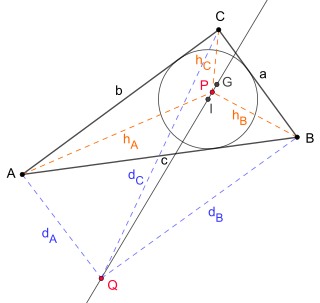
The equal detour point is a triangle center with the Kimberling number X(176). It is characterized by the equal detour property, that is if you travel from any vertex of a triangle to another by taking a detour through some inner point then the additional distance travelled is constant. This means the following equation has to hold:

In geometry, the Feuerbach hyperbola is a rectangular hyperbola passing through important triangle centers such as the Orthocenter, Gergonne point, Nagel point and Shiffler point. The center of the hyperbola is the Feuerbach point, the point of tangency of the incircle and the nine-point circle.
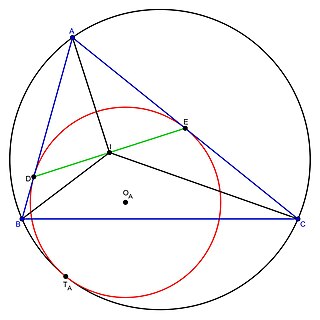
In plane geometry, a mixtilinear incircle of a triangle is a circle which is tangent to two of its sides and internally tangent to its circumcircle. The mixtilinear incircle of a triangle tangent to the two sides containing vertex is called the -mixtilinear incircle. Every triangle has three unique mixtilinear incircles, one corresponding to each vertex.
In Euclidean geometry, the Neuberg cubic is a special cubic plane curve associated with a reference triangle with several remarkable properties. It is named after Joseph Jean Baptiste Neuberg, a Luxembourger mathematician, who first introduced the curve in a paper published in 1884. The curve appears as the first item, with identification number K001, in Bernard Gilbert's Catalogue of Triangle Cubics which is a compilation of extensive information about more than 1200 triangle cubics.
In Euclidean geometry, the McCay cubic is a cubic plane curve in the plane of a reference triangle and associated with it. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003.

In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.