![r
=
sin
[?]
th
th
,
-
20
<
th
<
20
{\displaystyle r={\frac {\sin \theta }{\theta }},-20<\theta <20} Cochleoid with a=1.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/4/41/Cochleoid_with_a%3D1.svg/420px-Cochleoid_with_a%3D1.svg.png)
A cochleoid is a snail-shaped curve similar to a strophoid which can be represented by the polar equation
Contents
or the parametric equations
The cochleoid is the inverse curve of Hippias' quadratrix. [1]
A cochleoid is a snail-shaped curve similar to a strophoid which can be represented by the polar equation
or the parametric equations
The cochleoid is the inverse curve of Hippias' quadratrix. [1]
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. The radial coordinate is often denoted by r or ρ, and the angular coordinate by φ, θ, or t. Angles in polar notation are generally expressed in either degrees or radians.
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuthal angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system.
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point.
A tautochrone or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to π times the square root of the radius over the acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid.
In geometry, an epicycloid or hypercycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an epicycle—which rolls without slipping around a fixed circle. It is a particular kind of roulette.
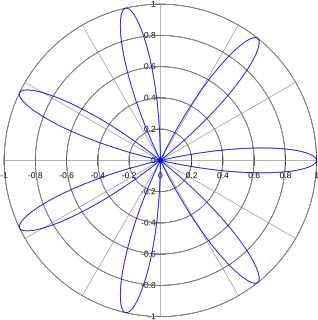
In mathematics, a rose or rhodonea curve is a sinusoid plotted in polar coordinates.
In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the point on the circle opposite to the point of tangency. In fact, the curve family of cissoids is named for this example and some authors refer to it simply as the cissoid. It has a single cusp at the pole, and is symmetric about the diameter of the circle which is the line of tangency of the cusp. The line is an asymptote. It is a member of the conchoid of de Sluze family of curves and in form it resembles a tractrix.
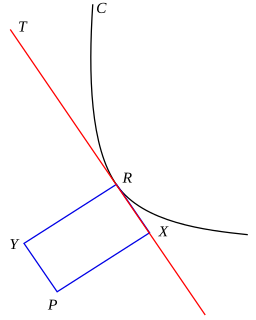
The pedal curve results from the orthogonal projection of a fixed point on the tangent lines of a given curve. More precisely, for a plane curve C and a given fixed pedal pointP, the pedal curve of C is the locus of points X so that the line PX is perpendicular to a tangent T to the curve passing through the point X. Conversely, at any point R on the curve C, let T be the tangent line at that point R; then there is a unique point X on the tangent T which forms with the pedal point P a line perpendicular to the tangent T – the pedal curve is the set of such points X, called the foot of the perpendicular to the tangent T from the fixed point P, as the variable point R ranges over the curve C.
Projectile motion is a form of motion experienced by an object or particle that is projected near the Earth's surface and moves along a curved path under the action of gravity only. This curved path was shown by Galileo to be a parabola, but may also be a line in the special case when it is thrown directly upwards. The study of such motions is called ballistics, and such a trajectory is a ballistic trajectory. The only force of significance that acts on the object is gravity, which acts downward, thus imparting to the object a downward acceleration. Because of the object's inertia, no external horizontal force is needed to maintain the horizontal velocity component of the object. Taking other forces into account, such as friction from aerodynamic drag or internal propulsion such as in a rocket, requires additional analysis. A ballistic missile is a missile only guided during the relatively brief initial powered phase of flight, and whose subsequent course is governed by the laws of classical mechanics.
In geometry, a cissoid is a curve generated from two given curves C1, C2 and a point O. Let L be a variable line passing through O and intersecting C1 at P1 and C2 at P2. Let P be the point on L so that OP = P1P2. Then the locus of such points P is defined to be the cissoid of the curves C1, C2 relative to O.
In geometry, a strophoid is a curve generated from a given curve C and points A and O as follows: Let L be a variable line passing through O and intersecting C at K. Now let P1 and P2 be the two points on L whose distance from K is the same as the distance from A to K. The locus of such points P1 and P2 is then the strophoid of C with respect to the pole O and fixed point A. Note that AP1 and AP2 are at right angles in this construction.
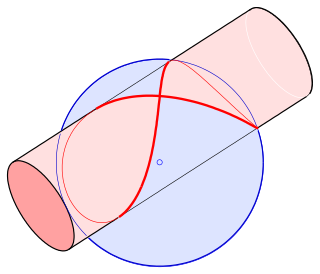
In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through the center of the sphere. Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.
The butterfly curve is a transcendental plane curve discovered by Temple H. Fay of University of Southern Mississippi in 1989.
The main trigonometric identities between trigonometric functions are proved, using mainly the geometry of the right triangle. For greater and negative angles, see Trigonometric functions.
In geometry, the Tschirnhausen cubic, or Tschirnhaus' cubic is a plane curve defined, in its left-opening form, by the polar equation
In inversive geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·OQ = k2. The inverse of the curve C is then the locus of P as Q runs over C. The point O in this construction is called the center of inversion, the circle the circle of inversion, and k the radius of inversion.
In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis.
For a plane curve C and a given fixed point O, the pedal equation of the curve is a relation between r and p where r is the distance from O to a point on C and p is the perpendicular distance from O to the tangent line to C at the point. The point O is called the pedal point and the values r and p are sometimes called the pedal coordinates of a point relative to the curve and the pedal point. It is also useful to measure the distance of O to the normal even though it is not an independent quantity and it relates to as .
 | Wikimedia Commons has media related to Cochleoid . |
 | This geometry-related article is a stub. You can help Wikipedia by expanding it. |