
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

The history of mathematics deals with the origin of discoveries in mathematics and the mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. From 3000 BC the Mesopotamian states of Sumer, Akkad and Assyria, followed closely by Ancient Egypt and the Levantine state of Ebla began using arithmetic, algebra and geometry for purposes of taxation, commerce, trade and also in the field of astronomy to record time and formulate calendars.

August Ferdinand Möbius was a German mathematician and theoretical astronomer.

Frank Morley was a leading mathematician, known mostly for his teaching and research in the fields of algebra and geometry. Among his mathematical accomplishments was the discovery and proof of the celebrated Morley's trisector theorem in elementary plane geometry.

Robert Daniel Carmichael was an American mathematician.
Donald Clayton Spencer was an American mathematician, known for work on deformation theory of structures arising in differential geometry, and on several complex variables from the point of view of partial differential equations. He was born in Boulder, Colorado, and educated at the University of Colorado and MIT.

Geometry of Complex Numbers is an undergraduate textbook on geometry, whose topics include circles, the complex plane, inversive geometry, and non-Euclidean geometry. It was written by Hans Schwerdtfeger, and originally published in 1962 as Volume 13 of the Mathematical Expositions series of the University of Toronto Press. A corrected edition was published in 1979 in the Dover Books on Advanced Mathematics series of Dover Publications (ISBN 0-486-63830-8), including the subtitle Circle Geometry, Moebius Transformation, Non-Euclidean Geometry. The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries.
In geometry, a cevian is a line segment which joins a vertex of a triangle to a point on the opposite side of the triangle. Medians and angle bisectors are special cases of cevians. The name "cevian" comes from the Italian mathematician Giovanni Ceva, who proved a well-known theorem about cevians which also bears his name.
Howard Jerome Keisler is an American mathematician, currently professor emeritus at University of Wisconsin–Madison. His research has included model theory and non-standard analysis.
In geometry, the compass equivalence theorem is an important statement in compass and straightedge constructions. The tool advocated by Plato in these constructions is a divider or collapsing compass, that is, a compass that "collapses" whenever it is lifted from a page, so that it may not be directly used to transfer distances. The modern compass with its fixable aperture can be used to transfer distances directly and so appears to be a more powerful instrument. However, the compass equivalence theorem states that any construction via a "modern compass" may be attained with a collapsing compass. This can be shown by establishing that with a collapsing compass, given a circle in the plane, it is possible to construct another circle of equal radius, centered at any given point on the plane. This theorem is Proposition II of Book I of Euclid's Elements. The proof of this theorem has had a chequered history.
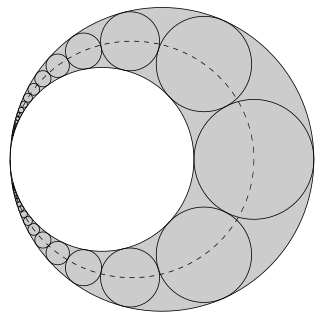
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.

Simon de la Loubère was a French diplomat to Siam (Thailand), writer, mathematician and poet. He is credited with bringing back a document which introduced Europe to Indian astronomy, the "Siamese method" of making magic squares, as well as one of the earliest description of parachutes.

Elementary Calculus: An Infinitesimal approach is a textbook by H. Jerome Keisler. The subtitle alludes to the infinitesimal numbers of the hyperreal number system of Abraham Robinson and is sometimes given as An approach using infinitesimals. The book is available freely online and is currently published by Dover.
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

Gary Theodore Chartrand is an American-born mathematician who specializes in graph theory. He is known for his textbooks on introductory graph theory and for the concept of a highly irregular graph.
Zeev Nehari was a mathematician who worked on Complex Analysis, Univalent Functions Theory and Differential and Integral Equations. He was a student of Michael (Mihály) Fekete. The Nehari manifold is named after him.
James Dugundji was an American mathematician, a professor of mathematics at the University of Southern California.
In mathematics, a Carlyle circle is a certain circle in a coordinate plane associated with a quadratic equation; it is named after Thomas Carlyle. The circle has the property that the solutions of the quadratic equation are the horizontal coordinates of the intersections of the circle with the horizontal axis. Carlyle circles have been used to develop ruler-and-compass constructions of regular polygons.
Doris J. Schattschneider is an American mathematician, a retired professor of mathematics at Moravian College. She is known for writing about tessellations and about the art of M. C. Escher, for helping Martin Gardner validate and popularize the pentagon tiling discoveries of amateur mathematician Marjorie Rice, and for co-directing with Eugene Klotz the project that developed The Geometer's Sketchpad.
Marvin David Marcus was an American mathematician, known as a leading expert on linear and multilinear algebra.











