Example game
In the following game, the first of the two players is using red, and the second is using blue. The last move in each image is shown brighter than the other areas.
The first player may colour any of the areas to begin. However, the region around the outside of the graph is not included as an area for this game.
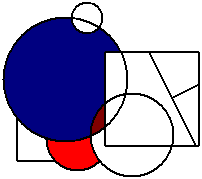
The second player now colours a white cell. As no areas are currently blue, any white cell is allowed.
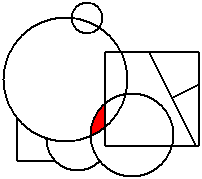
At this point, the requirement that the graph be proper comes into effect, as a red area must be made which does not touch the existing one:
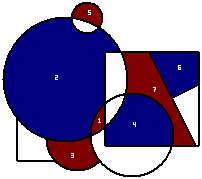
Once the third region is coloured:
Note that areas only count as touching if they share edges, not if they only share vertices, so this move is legal.
The game continues, players moving alternately, until one player cannot make a move. This player loses. A possible continuation of the game is as follows (with each move numbered for clarity):
In this outcome, the blue player has lost.