Color confinement

Last updated December 02, 2023

In quantum chromodynamics (QCD), color confinement, often simply called confinement, is the phenomenon that color-charged particles (such as quarks and gluons) cannot be isolated, and therefore cannot be directly observed in normal conditions below the Hagedorn temperature of approximately 2 tera kelvin (corresponding to energies of approximately 130–140 MeV per particle).^[1]^[2] Quarks and gluons must clump together to form hadrons. The two main types of hadron are the mesons (one quark, one antiquark) and the baryons (three quarks). In addition, colorless glueballs formed only of gluons are also consistent with confinement, though difficult to identify experimentally. Quarks and gluons cannot be separated from their parent hadron without producing new hadrons.^[3]

Origin

There is not yet an analytic proof of color confinement in any non-abelian gauge theory. The phenomenon can be understood qualitatively by noting that the force-carrying gluons of QCD have color charge, unlike the photons of quantum electrodynamics (QED). Whereas the electric field between electrically charged particles decreases rapidly as those particles are separated, the gluon field between a pair of color charges forms a narrow flux tube (or string) between them. Because of this behavior of the gluon field, the strong force between the particles is constant regardless of their separation.^[4]^[5]

Therefore, as two color charges are separated, at some point it becomes energetically favorable for a new quark–antiquark pair to appear, rather than extending the tube further. As a result of this, when quarks are produced in particle accelerators, instead of seeing the individual quarks in detectors, scientists see "jets" of many color-neutral particles (mesons and baryons), clustered together. This process is called hadronization , fragmentation, or string breaking.

The confining phase is usually defined by the behavior of the action of the Wilson loop, which is simply the path in spacetime traced out by a quark–antiquark pair created at one point and annihilated at another point. In a non-confining theory, the action of such a loop is proportional to its perimeter. However, in a confining theory, the action of the loop is instead proportional to its area. Since the area is proportional to the separation of the quark–antiquark pair, free quarks are suppressed. Mesons are allowed in such a picture, since a loop containing another loop with the opposite orientation has only a small area between the two loops. At non-zero temperatures, the order operator for confinement are thermal versions of Wilson loops known as Polyakov loops.

Confinement scale

The confinement scale or QCD scale is the scale at which the perturbatively defined strong coupling constant diverges. This is known as the Landau pole. The confinement scale definition and value therefore depend on the renormalization scheme used. For example, in the MS-bar scheme and at 4-loop in the running of $\alpha _{s}$ , the world average in the 3-flavour case is given by^[6]

\Lambda _{\overline {MS}}^{(3)}=(332\pm 17)\,{\rm {{MeV}\,.}}

When the renormalization group equation is solved exactly, the scale is not defined at all.^{[ clarification needed ]} It is therefore customary to quote the value of the strong coupling constant at a particular reference scale instead.

It is sometimes believed that the sole origin of confinement is the very large value of the strong coupling near the Landau pole. This is sometimes referred as infrared slavery (a term chosen to contrast with the ultraviolet freedom). It is however incorrect since in QCD the Landau pole is unphysical,^[7]^[8] which can be seen by the fact that its position at the confinement scale largely depends on the chosen renormalization scheme, i.e., on a convention. Most evidences point to a moderately large coupling, typically of value 1-3 ^[7] depending on the choice of renormalization scheme. In contrast to the simple but erroneous mechanism of infrared slavery, a large coupling is but one ingredient for color confinement, the other one being that gluons are color-charged and can therefore collapse into gluon tubes.

Models exhibiting confinement

In addition to QCD in four spacetime dimensions, the two-dimensional Schwinger model also exhibits confinement.^[9] Compact Abelian gauge theories also exhibit confinement in 2 and 3 spacetime dimensions.^[10] Confinement has been found in elementary excitations of magnetic systems called spinons.^[11]

If the electroweak symmetry breaking scale were lowered, the unbroken SU(2) interaction would eventually become confining. Alternative models where SU(2) becomes confining above that scale are quantitatively similar to the Standard Model at lower energies, but dramatically different above symmetry breaking.^[12]

Models of fully screened quarks

Besides the quark confinement idea, there is a potential possibility that the color charge of quarks gets fully screened by the gluonic color surrounding the quark. Exact solutions of SU(3) classical Yang–Mills theory which provide full screening (by gluon fields) of the color charge of a quark have been found.^[13] However, such classical solutions do not take into account non-trivial properties of QCD vacuum. Therefore, the significance of such full gluonic screening solutions for a separated quark is not clear.

Related Research Articles

A gluon is a type of elementary particle that mediates the strong interaction between quarks, acting as the exchange particle for the interaction. Gluons are massless vector bosons, thereby having a spin of 1. Through the strong interaction, gluons bind quarks into groups according to quantum chromodynamics (QCD), forming hadrons such as protons and neutrons.

<span class="mw-page-title-main">Hadron</span> Composite subatomic particle

In particle physics, a hadron is a composite subatomic particle made of two or more quarks held together by the strong interaction. They are analogous to molecules that are held together by the electric force. Most of the mass of ordinary matter comes from two hadrons: the proton and the neutron, while most of the mass of the protons and neutrons is in turn due to the binding energy of their constituent quarks, due to the strong force.

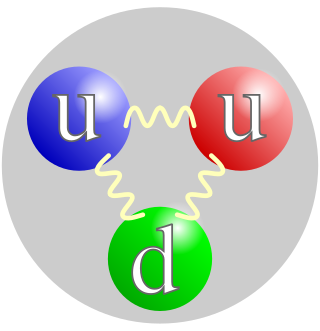
A quark is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly observable matter is composed of up quarks, down quarks and electrons. Owing to a phenomenon known as color confinement, quarks are never found in isolation; they can be found only within hadrons, which include baryons and mesons, or in quark–gluon plasmas. For this reason, much of what is known about quarks has been drawn from observations of hadrons.

In theoretical physics, quantum chromodynamics (QCD) is the theory of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type of quantum field theory called a non-abelian gauge theory, with symmetry group SU(3). The QCD analog of electric charge is a property called color. Gluons are the force carriers of the theory, just as photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of particle physics. A large body of experimental evidence for QCD has been gathered over the years.

Color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics (QCD).

In particle physics, the baryon number is a strictly conserved additive quantum number of a system. It is defined as

In quantum field theory, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become asymptotically weaker as the energy scale increases and the corresponding length scale decreases.

In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice.

Lattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics (QCD) theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time. When the size of the lattice is taken infinitely large and its sites infinitesimally close to each other, the continuum QCD is recovered.

Quark matter or QCD matter refers to any of a number of hypothetical phases of matter whose degrees of freedom include quarks and gluons, of which the prominent example is quark-gluon plasma. Several series of conferences in 2019, 2020, and 2021 were devoted to this topic.

The QCD vacuum is the quantum vacuum state of quantum chromodynamics (QCD). It is an example of a non-perturbative vacuum state, characterized by non-vanishing condensates such as the gluon condensate and the quark condensate in the complete theory which includes quarks. The presence of these condensates characterizes the confined phase of quark matter.

<span class="mw-page-title-main">Exotic hadron</span> Subatomic particles consisting of quarks and gluons

Exotic hadrons are subatomic particles composed of quarks and gluons, but which – unlike "well-known" hadrons such as protons, neutrons and mesons – consist of more than three valence quarks. By contrast, "ordinary" hadrons contain just two or three quarks. Hadrons with explicit valence gluon content would also be considered exotic. In theory, there is no limit on the number of quarks in a hadron, as long as the hadron's color charge is white, or color-neutral.

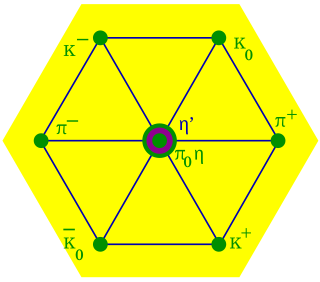
<span class="mw-page-title-main">Quark model</span> Classification scheme of hadrons

In particle physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks that give rise to the quantum numbers of the hadrons. The quark model underlies "flavor SU(3)", or the Eightfold Way, the successful classification scheme organizing the large number of lighter hadrons that were being discovered starting in the 1950s and continuing through the 1960s. It received experimental verification beginning in the late 1960s and is a valid effective classification of them to date. The model was independently proposed by physicists Murray Gell-Mann, who dubbed them "quarks" in a concise paper, and George Zweig, who suggested "aces" in a longer manuscript. André Petermann also touched upon the central ideas from 1963 to 1965, without as much quantitative substantiation. Today, the model has essentially been absorbed as a component of the established quantum field theory of strong and electroweak particle interactions, dubbed the Standard Model.

In particle physics, the parton model is a model of hadrons, such as protons and neutrons, proposed by Richard Feynman. It is useful for interpreting the cascades of radiation produced from quantum chromodynamics (QCD) processes and interactions in high-energy particle collisions.

In theoretical physics, the anti-de Sitter/quantum chromodynamics correspondence is a goal to describe quantum chromodynamics (QCD) in terms of a dual gravitational theory, following the principles of the AdS/CFT correspondence in a setup where the quantum field theory is not a conformal field theory.

Hadron spectroscopy is the subfield of particle physics that studies the masses and decays of hadrons. Hadron spectroscopy is also an important part of the new nuclear physics. The properties of hadrons are a consequence of a theory called quantum chromodynamics (QCD).

<span class="mw-page-title-main">Light front holography</span> Technique used to determine mass of hadrons

In strong interaction physics, light front holography or light front holographic QCD is an approximate version of the theory of quantum chromodynamics (QCD) which results from mapping the gauge theory of QCD to a higher-dimensional anti-de Sitter space (AdS) inspired by the AdS/CFT correspondence proposed for string theory. This procedure makes it possible to find analytic solutions in situations where strong coupling occurs, improving predictions of the masses of hadrons and their internal structure revealed by high-energy accelerator experiments. The most widely used approach to finding approximate solutions to the QCD equations, lattice QCD, has had many successful applications; however, it is a numerical approach formulated in Euclidean space rather than physical Minkowski space-time.

In theoretical particle physics, the gluon field is a four-vector field characterizing the propagation of gluons in the strong interaction between quarks. It plays the same role in quantum chromodynamics as the electromagnetic four-potential in quantum electrodynamics – the gluon field constructs the gluon field strength tensor.

The light-front quantization of quantum field theories provides a useful alternative to ordinary equal-time quantization. In particular, it can lead to a relativistic description of bound systems in terms of quantum-mechanical wave functions. The quantization is based on the choice of light-front coordinates, where $plays the role of time and the corresponding spatial coordinate is . Here, is the ordinary time, is a Cartesian coordinate, and is the speed of light. The other two Cartesian coordinates, and, are untouched and often called transverse or perpendicular, denoted by symbols of the type . The choice of the frame of reference where the time and -axis are defined can be left unspecified in an exactly soluble relativistic theory, but in practical calculations some choices may be more suitable than others. The basic formalism is discussed elsewhere.$

Kenneth Alan Johnson was an American theoretical physicist. He was professor of physics at MIT, a leader in the study of quantum field theories and the quark substructure of matter. Johnson contributed to the understanding of symmetry and anomalies in quantum field theories and to models of quark confinement and dynamics in quantum chromodynamics.

References

↑ Barger, V.; Phillips, R. (1997). Collider Physics. Addison–Wesley. ISBN 978-0-201-14945-6.
↑ Greensite, J. (2011). An introduction to the confinement problem. Lecture Notes in Physics. Vol. 821. Springer. Bibcode:2011LNP...821.....G. doi:10.1007/978-3-642-14382-3. ISBN 978-3-642-14381-6.
↑ Wu, T.-Y.; Hwang, Pauchy W.-Y. (1991). Relativistic quantum mechanics and quantum fields. World Scientific. p. 321. ISBN 978-981-02-0608-6.
↑ Muta, T. (2009). Foundations of Quantum Chromodynamics: An introduction to perturbative methods in gauge theories. Lecture Notes in Physics. Vol. 78 (3rd ed.). World Scientific. ISBN 978-981-279-353-9.
↑ Smilga, A. (2001). Lectures on quantum chromodynamics. World Scientific. ISBN 978-981-02-4331-9.
↑ "Review on Quantum Chromodynamics" (PDF). Particle Data Group.
1 2 A. Deur, S. J. Brodsky and G. F. de Teramond, (2016) “The QCD Running Coupling” Prog. Part. Nucl. Phys. 90, 1
↑ D. Binosi, C. Mezrag, J. Papavassiliou, C. D. Roberts and J. Rodriguez-Quintero, (2017) “Process-independent strong running coupling” Phys. Rev. D 96, no. 5, 054026
↑ Wilson, Kenneth G. (1974). "Confinement of Quarks". Physical Review D. 10 (8): 2445–2459. Bibcode:1974PhRvD..10.2445W. doi:10.1103/PhysRevD.10.2445.
↑ Schön, Verena; Michael, Thies (2000). "2d Model Field Theories at Finite Temperature and Density (Section 2.5)". In Shifman, M. (ed.). At the Frontier of Particle Physics. pp. 1945–2032. arXiv: hep-th/0008175 . Bibcode:2001afpp.book.1945S. CiteSeerX 10.1.1.28.1108 . doi:10.1142/9789812810458_0041. ISBN 978-981-02-4445-3. S2CID 17401298.
↑ Lake, Bella; Tsvelik, Alexei M.; Notbohm, Susanne; Tennant, D. Alan; Perring, Toby G.; Reehuis, Manfred; Sekar, Chinnathambi; Krabbes, Gernot; Büchner, Bernd (2009). "Confinement of fractional quantum number particles in a condensed-matter system". Nature Physics . 6 (1): 50–55. arXiv: 0908.1038 . Bibcode:2010NatPh...6...50L. doi:10.1038/nphys1462. S2CID 18699704.
↑ Claudson, M.; Farhi, E.; Jaffe, R. L. (1 August 1986). "Strongly coupled standard model". Physical Review D. 34 (3): 873–887. Bibcode:1986PhRvD..34..873C. doi:10.1103/PhysRevD.34.873. PMID 9957220.
↑ Cahill, Kevin (1978). "Example of Color Screening". Physical Review Letters . 41 (9): 599–601. Bibcode:1978PhRvL..41..599C. doi:10.1103/PhysRevLett.41.599.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Barger, V.; Phillips, R. (1997). Collider Physics. Addison–Wesley. ISBN 978-0-201-14945-6.

[2] Greensite, J. (2011). An introduction to the confinement problem. Lecture Notes in Physics. Vol. 821. Springer. Bibcode:2011LNP...821.....G. doi:10.1007/978-3-642-14382-3. ISBN 978-3-642-14381-6.

[3] Wu, T.-Y.; Hwang, Pauchy W.-Y. (1991). Relativistic quantum mechanics and quantum fields. World Scientific. p. 321. ISBN 978-981-02-0608-6.

[4] Muta, T. (2009). Foundations of Quantum Chromodynamics: An introduction to perturbative methods in gauge theories. Lecture Notes in Physics. Vol. 78 (3rd ed.). World Scientific. ISBN 978-981-279-353-9.

[5] Smilga, A. (2001). Lectures on quantum chromodynamics. World Scientific. ISBN 978-981-02-4331-9.

[6] "Review on Quantum Chromodynamics" (PDF). Particle Data Group.

[alpha_s_review_2016-7] 1 2 A. Deur, S. J. Brodsky and G. F. de Teramond, (2016) “The QCD Running Coupling” Prog. Part. Nucl. Phys. 90, 1

[alpha_s_DSE_2016-8] D. Binosi, C. Mezrag, J. Papavassiliou, C. D. Roberts and J. Rodriguez-Quintero, (2017) “Process-independent strong running coupling” Phys. Rev. D 96, no. 5, 054026

[Wilson_1974-9] Wilson, Kenneth G. (1974). "Confinement of Quarks". Physical Review D. 10 (8): 2445–2459. Bibcode:1974PhRvD..10.2445W. doi:10.1103/PhysRevD.10.2445.

[10] Schön, Verena; Michael, Thies (2000). "2d Model Field Theories at Finite Temperature and Density (Section 2.5)". In Shifman, M. (ed.). At the Frontier of Particle Physics. pp. 1945–2032. arXiv: hep-th/0008175 . Bibcode:2001afpp.book.1945S. CiteSeerX 10.1.1.28.1108 . doi:10.1142/9789812810458_0041. ISBN 978-981-02-4445-3. S2CID 17401298.

[Lake_et_al,_2009-11] Lake, Bella; Tsvelik, Alexei M.; Notbohm, Susanne; Tennant, D. Alan; Perring, Toby G.; Reehuis, Manfred; Sekar, Chinnathambi; Krabbes, Gernot; Büchner, Bernd (2009). "Confinement of fractional quantum number particles in a condensed-matter system". Nature Physics . 6 (1): 50–55. arXiv: 0908.1038 . Bibcode:2010NatPh...6...50L. doi:10.1038/nphys1462. S2CID 18699704.

[12] Claudson, M.; Farhi, E.; Jaffe, R. L. (1 August 1986). "Strongly coupled standard model". Physical Review D. 34 (3): 873–887. Bibcode:1986PhRvD..34..873C. doi:10.1103/PhysRevD.34.873. PMID 9957220.

[Cahill_1978-13] Cahill, Kevin (1978). "Example of Color Screening". Physical Review Letters . 41 (9): 599–601. Bibcode:1978PhRvL..41..599C. doi:10.1103/PhysRevLett.41.599.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]