Colossal magnetoresistance

Last updated

Colossal magnetoresistance (CMR) is a property of some materials, mostly manganese-based perovskite oxides, that enables them to dramatically change their electrical resistance in the presence of a magnetic field. The magnetoresistance of conventional materials enables changes in resistance of up to 5%, but materials featuring CMR may demonstrate resistance changes by orders of magnitude. [1] [2]

Contents

This technology may find uses in disk read-and-write heads, allowing for increases in hard disk drive data density. However, so far it has not led to practical applications because it requires low temperatures and bulky equipment. [3] [4]

History

Initially discovered in mixed-valence perovskite manganites in the 1950s by G. H. Jonker and J. H. van Santen, [5] [6] a first theoretical description in terms of the double-exchange mechanism was given early on. In this model, the spin orientation of adjacent Mn moments is associated with kinetic exchange of eg-electrons. Consequently, alignment of the Mn spins by an external magnetic field causes higher conductivity. Relevant experimental work was done by Volger, [7] Wollan and Koehler, [8] and later on by Jirak et al. [9] and Pollert et al. [10]

However, the double exchange model did not adequately explain the high insulating-like resistivity above the transition temperature. [11] In the 1990s, work by R. von Helmolt et al. [12] and Jin et al. [13] initiated a large number of further studies. Although there is still no complete understanding of the phenomenon, there is a variety of theoretical and experimental work providing a deeper understanding of the relevant effects.

Theory

One prominent model is the so-called half-metallic ferromagnetic model, which is based on spin-polarized (SP) band structure calculations using the local spin-density approximation (LSDA) of the density functional theory (DFT) where separate calculations are carried out for spin-up and spin-down electrons. The half-metallic state is concurrent with the existence of a metallic majority spin band and a nonmetallic minority spin band in the ferromagnetic phase.

This model is not the same as the Stoner Model of itinerant ferromagnetism. In the Stoner model, a high density of states at the Fermi level makes the nonmagnetic state unstable. In SP calculations of covalent ferromagnets using DFT-LSDA functionals, the exchange-correlation integral takes the place of the Stoner parameter. The density of states at the Fermi level does not play a special role. [14] A significant advantage of the half-metallic model is that it does not rely on the presence of mixed valency as does the double exchange mechanism and it can therefore explain the observation of CMR in stoichiometric phases like the pyrochlore Tl
2Mn
2O
7. Microstructural effects in polycrystalline samples have also been investigated and it has been found that the magnetoresistance is often dominated by the tunneling of spin-polarized electrons between grains, resulting in the magnetoresistance having an intrinsic dependence on grain size. [15] [16]

A fully quantitative understanding of the CMR effect remains elusive and it is still the subject of much current research. Early promises of the development of new CMR-based technologies have not yet come to fruition.

See also

Related Research Articles

Magnetoresistance is the tendency of a material to change the value of its electrical resistance in an externally-applied magnetic field. There are a variety of effects that can be called magnetoresistance. Some occur in bulk non-magnetic metals and semiconductors, such as geometrical magnetoresistance, Shubnikov–de Haas oscillations, or the common positive magnetoresistance in metals. Other effects occur in magnetic metals, such as negative magnetoresistance in ferromagnets or anisotropic magnetoresistance (AMR). Finally, in multicomponent or multilayer systems, giant magnetoresistance (GMR), tunnel magnetoresistance (TMR), colossal magnetoresistance (CMR), and extraordinary magnetoresistance (EMR) can be observed.

Spintronics, also known as spin electronics, is the study of the intrinsic spin of the electron and its associated magnetic moment, in addition to its fundamental electronic charge, in solid-state devices. The field of spintronics concerns spin-charge coupling in metallic systems; the analogous effects in insulators fall into the field of multiferroics.

<span class="mw-page-title-main">Antiferromagnetism</span> Regular pattern of magnetic moment ordering

In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usually related to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism. The phenomenon of antiferromagnetism was first introduced by Lev Landau in 1933.

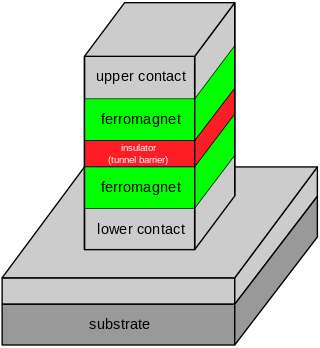
<span class="mw-page-title-main">Tunnel magnetoresistance</span> Magnetic effect in insulators between ferromagnets

Tunnel magnetoresistance (TMR) is a magnetoresistive effect that occurs in a magnetic tunnel junction (MTJ), which is a component consisting of two ferromagnets separated by a thin insulator. If the insulating layer is thin enough, electrons can tunnel from one ferromagnet into the other. Since this process is forbidden in classical physics, the tunnel magnetoresistance is a strictly quantum mechanical phenomenon, and lies in the study of spintronics.

<span class="mw-page-title-main">Giant magnetoresistance</span> Phenomenom involving the change of conductivity in metallic layers

Giant magnetoresistance (GMR) is a quantum mechanical magnetoresistance effect observed in multilayers composed of alternating ferromagnetic and non-magnetic conductive layers. The 2007 Nobel Prize in Physics was awarded to Albert Fert and Peter Grünberg for the discovery of GMR, which also sets the foundation for the study of spintronics.

In the physical theory of spin glass magnetization, the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction models the coupling of nuclear magnetic moments or localized inner d- or f-shell electron spins through conduction electrons. It is named after Malvin Ruderman, Charles Kittel, Tadao Kasuya, and Kei Yosida, the physicists who first proposed and developed the model.

Magnetic semiconductors are semiconductor materials that exhibit both ferromagnetism and useful semiconductor properties. If implemented in devices, these materials could provide a new type of control of conduction. Whereas traditional electronics are based on control of charge carriers, practical magnetic semiconductors would also allow control of quantum spin state. This would theoretically provide near-total spin polarization, which is an important property for spintronics applications, e.g. spin transistors.

Exchange bias or exchange anisotropy occurs in bilayers of magnetic materials where the hard magnetization behavior of an antiferromagnetic thin film causes a shift in the soft magnetization curve of a ferromagnetic film. The exchange bias phenomenon is of tremendous utility in magnetic recording, where it is used to pin the state of the readback heads of hard disk drives at exactly their point of maximum sensitivity; hence the term "bias."

<span class="mw-page-title-main">Heusler compound</span>

Heusler compounds are magnetic intermetallics with face-centered cubic crystal structure and a composition of XYZ (half-Heuslers) or X2YZ (full-Heuslers), where X and Y are transition metals and Z is in the p-block. The term derives from the name of German mining engineer and chemist Friedrich Heusler, who studied such a compound (Cu2MnAl) in 1903. Many of these compounds exhibit properties relevant to spintronics, such as magnetoresistance, variations of the Hall effect, ferro-, antiferro-, and ferrimagnetism, half- and semimetallicity, semiconductivity with spin filter ability, superconductivity, topological band structure and are actively studied as Thermoelectric materials. Their magnetism results from a double-exchange mechanism between neighboring magnetic ions. Manganese, which sits at the body centers of the cubic structure, was the magnetic ion in the first Heusler compound discovered. (See the Bethe–Slater curve for details of why this happens.)

<span class="mw-page-title-main">Double-exchange mechanism</span>

The double-exchange mechanism is a type of a magnetic exchange that may arise between ions in different oxidation states. First proposed by Clarence Zener, this theory predicts the relative ease with which an electron may be exchanged between two species and has important implications for whether materials are ferromagnetic, antiferromagnetic, or exhibit spiral magnetism. For example, consider the 180 degree interaction of Mn-O-Mn in which the Mn "eg" orbitals are directly interacting with the O "2p" orbitals, and one of the Mn ions has more electrons than the other. In the ground state, electrons on each Mn ion are aligned according to the Hund's rule:

<span class="mw-page-title-main">Half-metal</span>

A half-metal is any substance that acts as a conductor to electrons of one spin orientation, but as an insulator or semiconductor to those of the opposite orientation. Although all half-metals are ferromagnetic, most ferromagnets are not half-metals. Many of the known examples of half-metals are oxides, sulfides, or Heusler alloys. Types of half-metallic compounds theoretically predicted so far include some Heusler alloys, such as Co2FeSi, NiMnSb, and PtMnSb; some Si-containing half–Heusler alloys with Curie temperatures over 600 K, such as NiCrSi and PdCrSi; some transition-metal oxides, including rutile structured CrO2; some perovskites, such as LaMnO3 and SeMnO3; and a few more simply structured zincblende (ZB) compounds, including CrAs and superlattices. NiMnSb and CrO2 have been experimentally determined to be half-metals at very low temperatures.

<span class="mw-page-title-main">Lanthanum strontium manganite</span>

Lanthanum strontium manganite (LSM or LSMO) is an oxide ceramic material with the general formula La1−xSrxMnO3, where x describes the doping level.

Gallium manganese arsenide, chemical formula (Ga,Mn)As is a magnetic semiconductor. It is based on the world's second most commonly used semiconductor, gallium arsenide,, and readily compatible with existing semiconductor technologies. Differently from other dilute magnetic semiconductors, such as the majority of those based on II-VI semiconductors, it is not paramagnetic but ferromagnetic, and hence exhibits hysteretic magnetization behavior. This memory effect is of importance for the creation of persistent devices. In (Ga,Mn)As, the manganese atoms provide a magnetic moment, and each also acts as an acceptor, making it a p-type material. The presence of carriers allows the material to be used for spin-polarized currents. In contrast, many other ferromagnetic magnetic semiconductors are strongly insulating and so do not possess free carriers. (Ga,Mn)As is therefore a candidate as a spintronic material.

<span class="mw-page-title-main">Magnetic structure</span>

The term magnetic structure of a material pertains to the ordered arrangement of magnetic spins, typically within an ordered crystallographic lattice. Its study is a branch of solid-state physics.

<span class="mw-page-title-main">Superexchange</span> Strong coupling between two cations through an intermediary anion

Superexchange or Kramers–Anderson superexchange interaction, is a prototypical indirect exchange coupling between neighboring magnetic moments by virtue of exchanging electrons through a non-magnetic anion known as the superexchange center. In this way, it differs from direct exchange, in which there is direct overlap of electron wave function from nearest neighboring cations not involving an intermediary anion or exchange center. While direct exchange can be either ferromagnetic or antiferromagnetic, the superexchange interaction is usually antiferromagnetic, preferring opposite alignment of the connected magnetic moments. Similar to the direct exchange, superexchange calls for the combined effect of Pauli exclusion principle and Coulomb's repulsion of the electrons. If the superexchange center and the magnetic moments it connects to are non-collinear, namely the atomic bonds are canted, the superexchange will be accompanied by the antisymmetric exchange known as the Dzyaloshinskii–Moriya interaction, which prefers orthogonal alignment of neighboring magnetic moments. In this situation, the symmetric and antisymmetric contributions compete with each other and can result in versatile magnetic spin textures such as magnetic skyrmions.

Lanthanum manganite is an inorganic compound with the formula LaMnO3, often abbreviated as LMO. Lanthanum manganite is formed in the perovskite structure, consisting of oxygen octahedra with a central Mn atom. The cubic perovskite structure is distorted into an orthorhombic structure by a strong Jahn–Teller distortion of the oxygen octahedra.

Colossal magnetoresistance (CMR) is a property in many perovskite oxides. However, the requirement of large external magnetic field hinders the potential applications. On one hand, people were looking for the physical mechanisms for the CMR originality. On the other hand, people were trying to find alternative ways to further improve the CMR effect. Large magnetoresistance at relative low magnetic field had been reported in doped LaMnO3 polycrystal samples, rather than single crystal. The spin polarized tunneling and spin dependent scattering across large angle boundaries are responsible for the Low field magnetoresistance (LFMR).

<span class="mw-page-title-main">Manganese monosilicide</span> Chemical compound

Manganese monosilicide (MnSi) is an intermetallic compound, a silicide of manganese. It occurs in cosmic dust as the mineral brownleeite. MnSi has a cubic crystal lattice with no inversion center; therefore its crystal structure is helical, with right-hand and left-hand chiralities.

<span class="mw-page-title-main">Gang Cao</span> American physicist

Gang Cao is an American condensed matter physicist, academic, author, and researcher. He is a professor of physics at the University of Colorado Boulder. and Director of Center for Experiments on Quantum Materials.

Elbio Rubén Dagotto is an Argentinian-American theoretical physicist and academic. He is a distinguished professor in the department of physics and astronomy at the University of Tennessee, Knoxville, and Distinguished Scientist in the Materials Science and Technology Division at the Oak Ridge National Laboratory.

References

  1. ↑ Ramirez, A. P. (1997). "Colossal magnetoresistance". Journal of Physics: Condensed Matter. 9 (39): 8171–8199. Bibcode:1997JPCM....9.8171R. doi:10.1088/0953-8984/9/39/005. S2CID   19951846.
  2. ↑ Rodriguez-Martinez, L.; Attfield, J.P. (1996). "Cation disorder and size effects in magnetoresistive manganese oxide perovskites". Physical Review B. 54 (22): R15622–R15625. Bibcode:1996PhRvB..5415622R. doi:10.1103/PhysRevB.54.R15622. PMID   9985717.
  3. ↑ "Chemists exploring new material with 'next generation' computer hard drive possibilities". The University of Aberdeen News. 27 January 2014.
  4. ↑ Dagotto, Elbio (14 March 2013). "Brief Introduction to Giant Magnetoresistance (GMR)". Nanoscale Phase Separation and Colossal Magnetoresistance: The Physics of Manganites and Related Compounds. Springer Series in Solid-State Sciences. Vol. 136. Springer Science & Business Media. pp. 395–396. doi:10.1007/978-3-662-05244-0_21. ISBN   9783662052440.
  5. ↑ Jonker, G. H.; Van Santen, J. H. (1950). "Ferromagnetic compounds of manganese with perovskite structure". Physica. 16 (3): 337. Bibcode:1950Phy....16..337J. doi:10.1016/0031-8914(50)90033-4.
  6. ↑ Van Santen, J. H.; Jonker, G. H. (1950). "Electrical conductivity of ferromagnetic compounds of manganese with perovskite structure". Physica. 16 (7): 599–600. doi:10.1016/0031-8914(50)90104-2.
  7. ↑ Volger, J. (1954). "Further experimental investigations on some ferromagnetic oxidic compounds of manganese with perovskite structure". Physica. 20 (1): 49–66. Bibcode:1954Phy....20...49V. doi:10.1016/S0031-8914(54)80015-2.
  8. ↑ Wollan, E. O.; Koehler, W. C. (1955). "Neutron Diffraction Study of the Magnetic Properties of the Series of Perovskite-Type Compounds [(1-x)La, x Ca]MnO_{3}". Physical Review. 100 (2): 545. Bibcode:1955PhRv..100..545W. doi:10.1103/PhysRev.100.545.
  9. ↑ Jirák, Z.; Krupička, S.; Šimša, Z.; Dlouhá, M.; Vratislav, S. (1985). "Neutron diffraction study of Pr1 − xCaxMnO3 perovskites". Journal of Magnetism and Magnetic Materials. 53 (1–2): 153. Bibcode:1985JMMM...53..153J. doi:10.1016/0304-8853(85)90144-1.
  10. ↑ Pollert, E.; Krupička, S.; Kuzmičová, E. (1982). "Structural study of Pr1−xCaxMnO3 and Y1−xCaxMnO3 perovskites". Journal of Physics and Chemistry of Solids. 43 (12): 1137. Bibcode:1982JPCS...43.1137P. doi:10.1016/0022-3697(82)90142-1.
  11. ↑ Lalena, J.N.; Cleary, D.A. (2010). Principles of Inorganic Materials Design (2nd ed.). Wiley. p. 361. ISBN   9780470567531.
  12. ↑ von Helmolt, R.; Wecker, J.; Holzapfel, B.; Schultz, L.; Samwer, K. (1993). "Giant negative magnetoresistance in perovskitelike La2/3Ba1/3Mn Ox ferromagnetic films". Physical Review Letters. 71 (14): 2331–2333. Bibcode:1993PhRvL..71.2331V. doi:10.1103/PhysRevLett.71.2331. PMID   10054646.
  13. ↑ Jin, S.; Tiefel, T. H.; McCormack, M.; Fastnacht, R. A.; Ramesh, R.; Chen, L. H. (1994). "Thousandfold Change in Resistivity in Magnetoresistive La-Ca-Mn-O Films". Science. 264 (5157): 413–5. Bibcode:1994Sci...264..413J. doi:10.1126/science.264.5157.413. PMID   17836905. S2CID   39802144.
  14. ↑ Zeller, R. (419–445). Grotendorst, J.; Blũgel, S.; Marx, D. (eds.). Computational Nanoscience: Do It Yourself. NIC Series. Vol. 31. Jũlich: John von Neumann Institute for Computing. p. 2006. ISBN   3-00-017350-1.
  15. ↑ Lalena & Cleary 2010 , pp. 361–2
  16. ↑ For a review see:Dagotto, E. (2003). Nanoscale Phase Separation and Colossal Magnetoresistance. Springer Series in Solid-State Sciences. Springer. ISBN   978-3-662-05244-0.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.