
In computational chemistry, molecular physics, and physical chemistry, the Lennard-Jones potential is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is probably the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions. The Lennard-Jones potential is often used as a building block in molecular models for more complex substances. Many studies of the idealized "Lennard-Jones substance" use the potential to understand the physical nature of matter.

In materials science and solid mechanics, Poisson's ratioν (nu) is a measure of the Poisson effect, the deformation of a material in directions perpendicular to the specific direction of loading. The value of Poisson's ratio is the negative of the ratio of transverse strain to axial strain. For small values of these changes, ν is the amount of transversal elongation divided by the amount of axial compression. Most materials have Poisson's ratio values ranging between 0.0 and 0.5. For soft materials, such as rubber, where the bulk modulus is much higher than the shear modulus, Poisson's ratio is near 0.5. For open-cell polymer foams, Poisson's ratio is near zero, since the cells tend to collapse in compression. Many typical solids have Poisson's ratios in the range of 0.2 to 0.3. The ratio is named after the French mathematician and physicist Siméon Poisson.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In differential geometry, the Einstein tensor is used to express the curvature of a pseudo-Riemannian manifold. In general relativity, it occurs in the Einstein field equations for gravitation that describe spacetime curvature in a manner that is consistent with conservation of energy and momentum.
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.
The J-integral represents a way to calculate the strain energy release rate, or work (energy) per unit fracture surface area, in a material. The theoretical concept of J-integral was developed in 1967 by G. P. Cherepanov and independently in 1968 by James R. Rice, who showed that an energetic contour path integral was independent of the path around a crack.

In relativistic physics, the electromagnetic stress–energy tensor is the contribution to the stress–energy tensor due to the electromagnetic field. The stress–energy tensor describes the flow of energy and momentum in spacetime. The electromagnetic stress–energy tensor contains the negative of the classical Maxwell stress tensor that governs the electromagnetic interactions.
The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members often asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
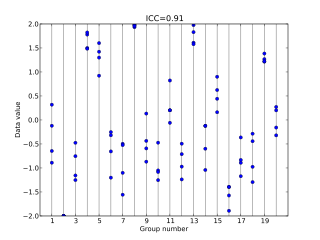
In statistics, the intraclass correlation, or the intraclass correlation coefficient (ICC), is a descriptive statistic that can be used when quantitative measurements are made on units that are organized into groups. It describes how strongly units in the same group resemble each other. While it is viewed as a type of correlation, unlike most other correlation measures, it operates on data structured as groups rather than data structured as paired observations.

Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.
In statistical mechanics, the eight-vertex model is a generalisation of the ice-type (six-vertex) models; it was discussed by Sutherland, and Fan & Wu, and solved by Baxter in the zero-field case.
Chapman–Enskog theory provides a framework in which equations of hydrodynamics for a gas can be derived from the Boltzmann equation. The technique justifies the otherwise phenomenological constitutive relations appearing in hydrodynamical descriptions such as the Navier–Stokes equations. In doing so, expressions for various transport coefficients such as thermal conductivity and viscosity are obtained in terms of molecular parameters. Thus, Chapman–Enskog theory constitutes an important step in the passage from a microscopic, particle-based description to a continuum hydrodynamical one.
In theoretical chemistry, the Buckingham potential is a formula proposed by Richard Buckingham which describes the Pauli exclusion principle and van der Waals energy for the interaction of two atoms that are not directly bonded as a function of the interatomic distance . It is a variety of interatomic potentials.

In mathematical physics, in particular electromagnetism, the Riemann–Silberstein vector or Weber vector named after Bernhard Riemann, Heinrich Martin Weber and Ludwik Silberstein, is a complex vector that combines the electric field E and the magnetic field B.
In the Newman–Penrose (NP) formalism of general relativity, independent components of the Ricci tensors of a four-dimensional spacetime are encoded into seven Ricci scalars which consist of three real scalars , three complex scalars and the NP curvature scalar . Physically, Ricci-NP scalars are related with the energy–momentum distribution of the spacetime due to Einstein's field equation.
Reynolds stress equation model (RSM), also referred to as second moment closures are the most complete classical turbulence model. In these models, the eddy-viscosity hypothesis is avoided and the individual components of the Reynolds stress tensor are directly computed. These models use the exact Reynolds stress transport equation for their formulation. They account for the directional effects of the Reynolds stresses and the complex interactions in turbulent flows. Reynolds stress models offer significantly better accuracy than eddy-viscosity based turbulence models, while being computationally cheaper than Direct Numerical Simulations (DNS) and Large Eddy Simulations.
Charge transport mechanisms are theoretical models that aim to quantitatively describe the electric current flow through a given medium.

In theoretical physics, the dual photon is a hypothetical elementary particle that is a dual of the photon under electric–magnetic duality which is predicted by some theoretical models, including M-theory.
The Galilei-covariant tensor formulation is a method for treating non-relativistic physics using the extended Galilei group as the representation group of the theory. It is constructed in the light cone of a five dimensional manifold.
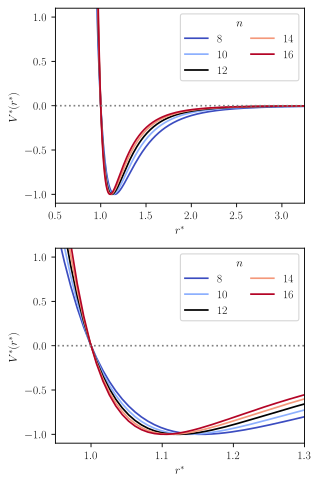
The Mie potential is an interaction potential describing the interactions between particles on the atomic level. It is mostly used for describing intermolecular interactions, but at times also for modeling intramolecular interaction, i.e. bonds.





























