Commentariolus

Last updated
De hypothesibus motuum coelestium a se constitutis commentariolus
Commentariolus Wien MS10530 Blatt 34.png
Ms. Austrian National Library, 10530, f. 34r
Author Nicolaus Copernicus
Language Latin
Subject Astronomy
Publication date
1514

The Commentariolus (Little Commentary) is Nicolaus Copernicus's brief outline of an early version of his revolutionary heliocentric theory of the universe. [1] After further long development of his theory, Copernicus published the mature version in 1543 in his landmark work, De revolutionibus orbium coelestium (On the Revolutions of the Heavenly Spheres).

Contents

Copernicus wrote the Commentariolus in Latin by 1514 and circulated copies to his friends and colleagues. [lower-alpha 1] It thus became known among Copernicus's contemporaries, though it was never printed during his lifetime. In 1533, Johann Albrecht Widmannstetter delivered a series of lectures in Rome outlining Copernicus' theory. Pope Clement VII and several Catholic cardinals heard the lectures and were interested in the theory. On 1 November 1536, Nikolaus von Schönberg, Archbishop of Capua and since the preceding year a cardinal, wrote to Copernicus from Rome and asked him for a copy of his writings "at the earliest possible moment". [4]

Although copies of the Commentariolus circulated for a time after Copernicus's death, [lower-alpha 2] it subsequently lapsed into obscurity, and its previous existence remained known only indirectly, until a surviving manuscript copy was discovered and published in the second half of the nineteenth century. [lower-alpha 3]

Summary

The Commentariolus is subdivided into eight sections (or chapters), of which all but the first bear brief descriptive titles. After a brief introduction, the first section states seven postulates from which Copernicus proposes to show that the apparent motion of the planets can be explained systematically. [7]

The seven postulates

  1. Celestial bodies do not all revolve around a single point.
  2. The centre of the Earth is the centre of the lunar sphere—the orbit of the Moon around the Earth.
  3. All the spheres rotate around the Sun, which is near the centre of the Universe.
  4. The distance between the Earth and the Sun is an insignificant fraction of the distance from the Earth and the Sun to the stars, so parallax is not observed in the stars.
  5. The stars are immovable; their apparent daily motion is caused by the daily rotation of the Earth.
  6. The Earth is moved in a sphere around the Sun, causing the apparent annual migration of the Sun; the Earth has more than one motion.
  7. The Earth’s orbital motion around the Sun causes the seeming reverse in direction of the motions of the planets.

The remaining seven sections are titled, in order, De ordine orbium ("The order of the spheres"), De motibus qui circa solem apparent ("The apparent motions of the Sun"), Quod aequalitas motum non ad aequinoctia sed ad stellas fixas referatur ("Equal motion should be measured not by the equinoxes but by the fixed stars"), De Luna ("The Moon"), De tribus superioribus: Saturno, Jove et Marte ("The outer planets: Saturn, Jupiter and Mars"), De Venere ("Venus") and De Mercurio ("Mercury"). [8]

The order of the spheres

In this section, the heavenly spheres are given in order from outermost to innermost. The outermost sphere is that of the fixed stars, which remains perfectly stationary. Then follow those of Saturn, Jupiter, Mars, Earth, Venus and Mercury, which each revolve about the Sun from west to east with successively shorter periods of revolution, Saturn's being between 29 and 30 years, Jupiter's between 11 and 12, Mars's between 2 and 3, Earth's exactly one, Venus's between 8 and 9 months, [lower-alpha 4] and Mercury's between 2 and 3 months. The Moon's sphere, however, revolves around the Earth in a period of one month, and moves with it around the Sun like an epicycle.

The apparent motion of the Sun

This section explains how the apparent motion of the Sun could arise from three separate motions of the Earth. The first motion is a uniform revolution, with a period of one year, from west to east along a circular orbit whose centre is offset from the Sun by 1/25 of the orbit's radius.

The second motion is the daily rotation about an axis which passes through the Earth's centre and is inclined at an angle of about 231⁄2° to the perpendicular to the plane of its orbit.

The third motion is a precession of the Earth's axis of rotation about an axis perpendicular to the plane of its orbit. Copernicus specified the rate of this precession with respect to the radial line from the Earth to the centre of its orbit as being slightly less than a year, with an implied direction as being from west to east. With respect to the fixed stars, this precession is very slow, and in the opposite direction—from east to west—and explains the phenomenon of the precession of the equinoxes.

Equal motion should be measured not by the equinoxes but by the fixed stars

Here Copernicus asserts that the motion of the equinoxes and celestial poles has not been uniform, and argues that consequently they should not be used to define the reference frame with respect to which the motions of the planets are measured, and that the periods of the various planetary motions are more accurately determinable if those motions are measured with respect to the fixed stars. He maintains that he had found the length of the sidereal year to have always been 365 days 6 hours and 10 minutes. [lower-alpha 5]

The Moon

Diagram of the Moon's orbit, as described by Copernicus in his Commentariolus Commentariolus moon.jpeg
Diagram of the Moon's orbit, as described by Copernicus in his Commentariolus

Including the annual revolution around the Sun, which the Moon shares with the Earth in his system, Copernicus explains the Moon's motion as composed of five independent motions. Its motion around the Earth lies in a plane which is inclined at an angle of 5° to the plane of the Earth's orbit, and which precesses from east to west around an axis perpendicular to that plane, with a period of between 18 and 19 years with respect to the fixed stars. The remaining three motions, which take place within this orbital plane, are depicted in the diagram to the right. The first of these is that of the first, and larger, of two epicycles, whose center (represented by the point e1 in the diagram) moves uniformly from west to east around the circumference of a deferent centred on the Earth (represented by point T in the diagram), with a period of one draconitic month. [lower-alpha 6] The centre of the second, smaller epicycle (represented by the point e2 in the diagram) moves uniformly from east to west around the circumference of the first so that the period of the angle β in the diagram is one anomalistic month. [9]

The Moon itself, represented by the point M in the diagram, moves uniformly from west to east around the circumference of the second epicycle so that the period of the angle γ is half a synodic month. [9] Copernicus states that whenever the point e1 lies on the line joining the Earth to the centre of its orbit (represented by the dotted line OTC in the diagram, of which only the point T here lies in the Moon's orbital plane), the Moon M will lie precisely between e1 and e2. However, this can occur only once every 19 years, when this line coincides with the line of nodes WTE. At other times it does not lie in the moon's orbital plane and the point e1 cannot therefore pass through it. In general, then, while the Moon will be close to conjunction or opposition to the Sun whenever it lies precisely between e1 and e2, these events will not be precisely simultaneous.

The ratio which Copernicus took as that for the relative lengths of the small epicycle, large epicycle and deferent is 4:19:180.

The outer planets, Saturn, Jupiter and Mars

The theories Copernicus gives in the Commentariolus for the motions of the outer planets all have the same general structure, and only differ in the values of the various parameters needed to specify their motions completely. Their orbits are not coplanar with that of the Earth, but do share its centre as their own common centre, and lie in planes that are only slightly inclined to the Earth's orbital plane. Unlike the Moon's orbital plane, those of the superior planets do not precess. Their inclinations to the Earth's orbital plane do oscillate, however, between the limits 0°10′ and 1°50′ for Mars, 1°15′ and 1°40′ for Jupiter, and 2°15′ and 2°40′ for Saturn. Although Copernicus supposes these oscillations to take place around the orbits' lines of nodes that he assumes to remain fixed, the mechanism he uses to model them does cause tiny oscillations in the lines of nodes as well. As Kepler later pointed out, the necessity for assuming oscillations in the inclinations of the outer planets' orbital planes is an artefact of Copernicus's having taken them as passing through the centre of the Earth's orbit. If he had taken them as passing through the Sun, he would not have needed to introduce these oscillations. [10]

Diagram of an outer planet's orbit, as described by Copernicus in his Commentariolus Commentariolus outer planets.jpeg
Diagram of an outer planet's orbit, as described by Copernicus in his Commentariolus

Like the Moon's motion, that of the outer planets, represented in the diagram to the right, is produced by a combination of a deferent and two epicycles. The centre of the first, and larger of the two epicycles, represented by the point e1 in the diagram, revolves uniformly from west to east around the circumference of a deferent whose centre is the centre of the Earth's orbit, represented by the point S in the diagram, with a period relative to the fixed stars as given in the section The order of the spheres above.

The centre of the second epicycle, represented by the point e2 in the diagram, revolves uniformly from east to west around the circumference of the first, with the same period relative to the radial line joining S to e1. As a consequence, the direction of the radial line joining e1 to e2 remains fixed relative to the fixed stars, parallel to the planet's line of apses EW, and the point e2 describes an eccentric circle [lower-alpha 7] whose radius is equal to that of the deferent, and whose centre, represented by the point O in the diagram, is offset from that of the deferent by the radius of the first epicycle. In his later work, De revolutionibus orbium coelestium , Copernicus uses this eccentric circle directly, rather than representing it as a combination of a deferent and an epicycle.

The planet itself, represented by the point P in the diagram, revolves uniformly from west to east around the circumference of the second epicycle, whose radius is exactly one third of that of the first, at twice the rate of revolution of e1 about S. This device enabled Copernicus to dispense with the equant, a much-criticised feature of Claudius Ptolemy's theories for the motions of the outer planets. In a heliocentric version of Ptolemy's models, his equant would lie at the point Q in the diagram, offset along the line of apses EW from the point S by a distance one and a third times the radius of Copernicus's first epicycle. The centre of the planet's deferent, with the same radius as Copernicus's, would lie at the point C, mid-way between S and Q. The planet itself would lie at the point of intersection of this deferent with the line QP. While this point only coincides exactly with P whenever they are both at an apsis, [lower-alpha 8] the difference between their positions is always negligible in comparison with the inaccuracies inherent to both theories.

For the ratios of the radii of the outer planets' deferents to radius of the Earth, the Commentariolus gives 113⁄25 for Mars, 513⁄60 for Jupiter, and 97⁄30 for Saturn. For the ratios of the radii of their deferents to the radii of the larger of their epicycles, it gives 6138⁄167 for Mars, 12553⁄606 for Jupiter, and 11859⁄1181 for Saturn. [lower-alpha 9]

Venus

In the last two sections Copernicus talks about Venus and Mercury. The first has a system of circles and takes 9 months to complete a revolution.

Mercury

Mercury's orbit is harder than any of the other planets' to study because it is visible for only a few days a year. Mercury, just like Venus, has two epicycles, one greater than another. It takes almost three months to complete a revolution.

Notes

  1. ↑ A reference to the Commentariolus is contained in a library catalogue, dated 1 May 1514, of a 16th-century historian, Matthew of Miechow, so it must have begun circulating before that date. [2] [3]
  2. ↑ Tycho Brahe obtained a copy in 1575, and subsequently presented copies to students and colleagues as tokens of his esteem. [5] [6]
  3. ↑ According to Rosen (2004, pp. 6–7), a manuscript copy of the Commentariolus was discovered in Vienna and published in 1878. It was said by Koyré (1973, p. 76) that a very poor copy was published in the 1854 Warsaw edition of De revolutionibus. This seems to be a mistake.
  4. ↑ Copernicus does not specify which type of month he is referring to. His period for Venus would be correct if he were referring to tropical or sidereal months. Venus's period is, however, less than 8 synodic months.
  5. ↑ A value that lies within one minute of what it is now.
  6. ↑ The period referred to here is the time between two successive passages of the epicycle's centre through its ascending node (represented in the diagram by the point W), or two successive passages through its descending node (represented in the diagram by the point E). Copernicus does not always distinguish which periods and which types of month he is referring to, but these can be inferred from our knowledge of the actual motion of the Moon.
  7. ↑ That is, a circle whose centre is offset from what would be regarded as the natural centre of the planet's orbit—in this case, the centre of the Earth's orbit.
  8. ↑ At all other times it will lie strictly between Q and P.
  9. ↑ Copernicus does not give these ratios directly, but expresses the radii of the planets' deferents and epicycles in terms of a unit of length which is 1⁄25th of the radius of the Earth's orbit.

Related Research Articles

<span class="mw-page-title-main">Celestial sphere</span> Imaginary sphere of arbitrarily large radius, concentric with the observer

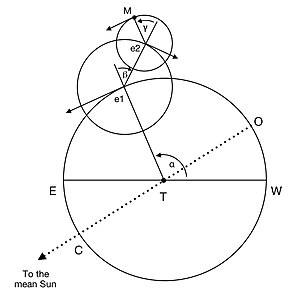
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, which may be centered on Earth or the observer. If centered on the observer, half of the sphere would resemble a hemispherical screen over the observing location.

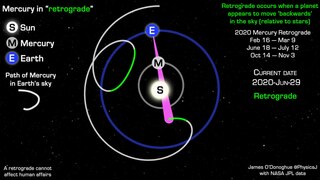
<span class="mw-page-title-main">Apparent retrograde motion</span> Apparent backward motion of a planet

Apparent retrograde motion is the apparent motion of a planet in a direction opposite to that of other bodies within its system, as observed from a particular vantage point. Direct motion or prograde motion is motion in the same direction as other bodies.

<span class="mw-page-title-main">Albert Brudzewski</span> Polish academic and diplomat (c. 1445 - c. 1497)

Albert Brudzewski, alsoAlbert Blar (of Brudzewo), Albert of Brudzewo or Wojciech Brudzewski (in Latin, Albertus de Brudzewo; c.1445–c.1497) was a Polish astronomer, mathematician, philosopher and diplomat.

<span class="mw-page-title-main">Aristarchus of Samos</span> Greek astronomer and mathematician (c.310–c.230 BC)

Aristarchus of Samos was an ancient Greek astronomer and mathematician who presented the first known heliocentric model that placed the Sun at the center of the universe, with the Earth revolving around the Sun once a year and rotating about its axis once a day.

<span class="mw-page-title-main">Geocentric model</span> Superseded description of the Universe with Earth at the center

In astronomy, the geocentric model is a superseded description of the Universe with Earth at the center. Under most geocentric models, the Sun, Moon, stars, and planets all orbit Earth. The geocentric model was the predominant description of the cosmos in many European ancient civilizations, such as those of Aristotle in Classical Greece and Ptolemy in Roman Egypt, as well as during the Islamic Golden Age.

<span class="mw-page-title-main">Deferent and epicycle</span> Planetary motions in archaic models of the Solar System

In the Hipparchian, Ptolemaic, and Copernican systems of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets. In particular it explained the apparent retrograde motion of the five planets known at the time. Secondarily, it also explained changes in the apparent distances of the planets from the Earth.

The orbital period is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.

<span class="mw-page-title-main">Tychonic system</span> Model of the Solar System proposed in 1588 by Tycho Brahe

The Tychonic system is a model of the universe published by Tycho Brahe in the late 16th century, which combines what he saw as the mathematical benefits of the Copernican system with the philosophical and "physical" benefits of the Ptolemaic system. The model may have been inspired by Valentin Naboth and Paul Wittich, a Silesian mathematician and astronomer. A similar cosmological model was independently proposed in the Hindu astronomical treatise Tantrasamgraha by Nilakantha Somayaji of the Kerala school of astronomy and mathematics.

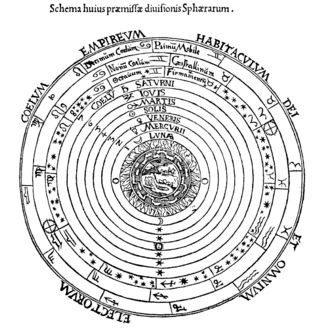
<span class="mw-page-title-main">Celestial spheres</span> Elements of some cosmological models

The celestial spheres, or celestial orbs, were the fundamental entities of the cosmological models developed by Plato, Eudoxus, Aristotle, Ptolemy, Copernicus, and others. In these celestial models, the apparent motions of the fixed stars and planets are accounted for by treating them as embedded in rotating spheres made of an aetherial, transparent fifth element (quintessence), like gems set in orbs. Since it was believed that the fixed stars did not change their positions relative to one another, it was argued that they must be on the surface of a single starry sphere.

<span class="mw-page-title-main">Equant</span> Outdated measure of planetary orbits

Equant is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of the planets. The equant is used to explain the observed speed change in different stages of the planetary orbit. This planetary concept allowed Ptolemy to keep the theory of uniform circular motion alive by stating that the path of heavenly bodies was uniform around one point and circular around another point.

<span class="mw-page-title-main">Fixed stars</span> Astronomical bodies that appear not to move relative to each other in the night sky

In astronomy, the fixed stars are the luminary points, mainly stars, that appear not to move relative to one another against the darkness of the night sky in the background. This is in contrast to those lights visible to naked eye, namely planets and comets, that appear to move slowly among those "fixed" stars.

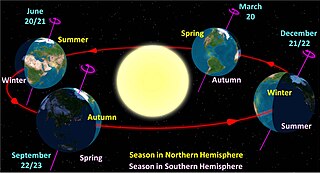
<span class="mw-page-title-main">Earth's orbit</span> Trajectory of Earth around the Sun

Earth orbits the Sun at an average distance of 149.60 million km in a counterclockwise direction as viewed from above the Northern Hemisphere. One complete orbit takes 365.256 days, during which time Earth has traveled 940 million km. Ignoring the influence of other Solar System bodies, Earth's orbit, also known as Earth's revolution, is an ellipse with the Earth-Sun barycenter as one focus with a current eccentricity of 0.0167. Since this value is close to zero, the center of the orbit is relatively close to the center of the Sun.

<i>De revolutionibus orbium coelestium</i> 1543 book by Copernicus describing his heliocentric theory of the universe

De revolutionibus orbium coelestium is the seminal work on the heliocentric theory of the astronomer Nicolaus Copernicus (1473–1543) of the Polish Renaissance. The book, first printed in 1543 in Nuremberg, Holy Roman Empire, offered an alternative model of the universe to Ptolemy's geocentric system, which had been widely accepted since ancient times.

<span class="mw-page-title-main">Copernican Revolution</span> 16th to 17th century intellectual revolution

The Copernican Revolution was the paradigm shift from the Ptolemaic model of the heavens, which described the cosmos as having Earth stationary at the center of the universe, to the heliocentric model with the Sun at the center of the Solar System. This revolution consisted of two phases; the first being extremely mathematical in nature and the second phase starting in 1610 with the publication of a pamphlet by Galileo. Beginning with the 1543 publication of Nicolaus Copernicus’s De revolutionibus orbium coelestium, contributions to the “revolution” continued until finally ending with Isaac Newton’s work over a century later.

<span class="mw-page-title-main">Ancient Greek astronomy</span> Astronomy as practiced in the Hellenistic world of classical antiquity

Ancient Greek astronomy is the astronomy written in the Greek language during classical antiquity. Greek astronomy is understood to include the Ancient Greek, Hellenistic, Greco-Roman, and late antique eras. Ancient Greek astronomy can be divided into three primary phases: Classical Greek Astronomy, which encompassed the 5th and 4th centuries BC, and Hellenistic Astronomy, which encompasses the subsequent period until the formation of the Roman Empire ca. 30 BC, and finally Greco-Roman astronomy, which refers to the continuation of the tradition of Greek astronomy in the Roman world. During the Hellenistic era and onwards, Greek astronomy expanded beyond the geographic region of Greece as the Greek language had become the language of scholarship throughout the Hellenistic world, in large part delimited by the boundaries of the Macedonian Empire established by Alexander the Great. The most prominent and influential practitioner of Greek astronomy was Ptolemy, whose treatise Almagest shaped astronomical thinking until the modern era. Most of the most prominent constellations known today are taken from Greek astronomy, albeit via the terminology they took on in Latin.

<span class="mw-page-title-main">Copernican heliocentrism</span> Heliocentric model of solar system by Nicolaus Copernicus

Copernican heliocentrism is the astronomical model developed by Nicolaus Copernicus and published in 1543. This model positioned the Sun at the center of the Universe, motionless, with Earth and the other planets orbiting around it in circular paths, modified by epicycles, and at uniform speeds. The Copernican model displaced the geocentric model of Ptolemy that had prevailed for centuries, which had placed Earth at the center of the Universe.

<span class="mw-page-title-main">Discovery and exploration of the Solar System</span>

Discovery and exploration of the Solar System is observation, visitation, and increase in knowledge and understanding of Earth's "cosmic neighborhood". This includes the Sun, Earth and the Moon, the major planets Mercury, Venus, Mars, Jupiter, Saturn, Uranus, and Neptune, their satellites, as well as smaller bodies including comets, asteroids, and dust.

Jacques du Chevreul was a French mathematician, astronomer, and philosopher.

<span class="mw-page-title-main">Historical models of the Solar System</span>

Historical models of the Solar System first appeared during prehistoric periods and are being updated to this day. The models of the Solar System throughout history were first represented in the early form of cave markings and drawings, calendars and astronomical symbols. Then books and written records became the main source of information that expressed the way the people of the time thought of the Solar System.

The Vicarious Hypothesis, or hypothesis vicaria, was a planetary hypothesis proposed by Johannes Kepler to describe the motion of Mars. The hypothesis adopted the circular orbit and equant of Ptolemy's planetary model as well as the heliocentrism of the Copernican model. Calculations using the Vicarious Hypothesis did not support a circular orbit for Mars, leading Kepler to propose elliptical orbits as one of three laws of planetary motion in Astronomia Nova.

References

  1. ↑ Koyré (1973 , pp. 18–28); Swerdlow (1973 , pp. 423–24); Copernicus (1992 , pp. 20, 208–52); Rosen (2004 , pp.  6–7 , 57–90 ).
  2. ↑ Koyré 1973, p. 85.
  3. ↑ Gingerich 2004, p. 32.
  4. ↑ Schönberg, Nicholas, Letter to Nicolaus Copernicus, translated by Edward Rosen.
  5. ↑ Dreyer 1890, p.  83.
  6. ↑ Thoren 1990, pp.  98–99.
  7. ↑ Goddu 2010, pp.  243-46).
  8. ↑ English translations by Rosen (2004 , pp.  57–65 ).
  9. 1 2 Swerdlow 1973, pp. 456–57.
  10. ↑ Swerdlow 1973, p. 486.

Bibliography

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.