Precession

Last updated October 06, 2024

.mw-parser-output .legend{page-break-inside:avoid;break-inside:avoid-column}.mw-parser-output .legend-color{display:inline-block;min-width:1.25em;height:1.25em;line-height:1.25;margin:1px 0;text-align:center;border:1px solid black;background-color:transparent;color:black}.mw-parser-output .legend-text{}
Rotation
Precession
Nutation
in obliquity of a planet Praezession.svg — Rotation
  Precession
   Nutation
in obliquity of a planet

Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In other words, if the axis of rotation of a body is itself rotating about a second axis, that body is said to be precessing about the second axis. A motion in which the second Euler angle changes is called nutation . In physics, there are two types of precession: torque-free and torque-induced.

Torque-free or torque neglected

Torque-free precession implies that no external moment (torque) is applied to the body. In torque-free precession, the angular momentum is a constant, but the angular velocity vector changes orientation with time. What makes this possible is a time-varying moment of inertia, or more precisely, a time-varying inertia matrix. The inertia matrix is composed of the moments of inertia of a body calculated with respect to separate coordinate axes (e.g. $x$ , $y$ , $z$ ). If an object is asymmetric about its principal axis of rotation, the moment of inertia with respect to each coordinate direction will change with time, while preserving angular momentum. The result is that the component of the angular velocities of the body about each axis will vary inversely with each axis' moment of inertia.

The torque-free precession rate of an object with an axis of symmetry, such as a disk, spinning about an axis not aligned with that axis of symmetry can be calculated as follows:^[1] ${\boldsymbol {\omega }}_{\mathrm {p} }={\frac {{\boldsymbol {I}}_{\mathrm {s} }{\boldsymbol {\omega }}_{\mathrm {s} }}{{\boldsymbol {I}}_{\mathrm {p} }\cos({\boldsymbol {\alpha }})}}$ where $ω p$ is the precession rate, $ω s$ is the spin rate about the axis of symmetry, $I s$ is the moment of inertia about the axis of symmetry, $I p$ is moment of inertia about either of the other two equal perpendicular principal axes, and $α$ is the angle between the moment of inertia direction and the symmetry axis.^[2]

When an object is not perfectly rigid, inelastic dissipation will tend to damp torque-free precession,^[3] and the rotation axis will align itself with one of the inertia axes of the body.

For a generic solid object without any axis of symmetry, the evolution of the object's orientation, represented (for example) by a rotation matrix $R$ that transforms internal to external coordinates, may be numerically simulated. Given the object's fixed internal moment of inertia tensor $I 0$ and fixed external angular momentum $L$ , the instantaneous angular velocity is ${\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)={\boldsymbol {R}}{\boldsymbol {I}}_{0}^{-1}{\boldsymbol {R}}^{T}{\boldsymbol {L}}$ Precession occurs by repeatedly recalculating $ω$ and applying a small rotation vector $ω dt$ for the short time $dt$ ; e.g.: ${\boldsymbol {R}}_{\text{new}}=\exp \left(\left[{\boldsymbol {\omega }}\left({\boldsymbol {R}}_{\text{old}}\right)\right]_{\times }dt\right){\boldsymbol {R}}_{\text{old}}$ for the skew-symmetric matrix $[ω] \times$ . The errors induced by finite time steps tend to increase the rotational kinetic energy: $E\left({\boldsymbol {R}}\right)={\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)\cdot {\frac {\boldsymbol {L}}{2}}$ this unphysical tendency can be counteracted by repeatedly applying a small rotation vector $v$ perpendicular to both $ω$ and $L$ , noting that $E\left(\exp \left(\left[{\boldsymbol {v}}\right]_{\times }\right){\boldsymbol {R}}\right)\approx E\left({\boldsymbol {R}}\right)+\left({\boldsymbol {\omega }}\left({\boldsymbol {R}}\right)\times {\boldsymbol {L}}\right)\cdot {\boldsymbol {v}}$

Torque-induced

Torque-induced precession (gyroscopic precession) is the phenomenon in which the axis of a spinning object (e.g., a gyroscope) describes a cone in space when an external torque is applied to it. The phenomenon is commonly seen in a spinning toy top, but all rotating objects can undergo precession. If the speed of the rotation and the magnitude of the external torque are constant, the spin axis will move at right angles to the direction that would intuitively result from the external torque. In the case of a toy top, its weight is acting downwards from its center of mass and the normal force (reaction) of the ground is pushing up on it at the point of contact with the support. These two opposite forces produce a torque which causes the top to precess.

The response of a rotating system to an applied torque. When the device swivels, and some roll is added, the wheel tends to pitch. Gyroscopic precession 256x256.png — The response of a rotating system to an applied torque. When the device swivels, and some roll is added, the wheel tends to pitch.

The device depicted on the right is gimbal mounted. From inside to outside there are three axes of rotation: the hub of the wheel, the gimbal axis, and the vertical pivot.

To distinguish between the two horizontal axes, rotation around the wheel hub will be called spinning, and rotation around the gimbal axis will be called pitching. Rotation around the vertical pivot axis is called rotation.

First, imagine that the entire device is rotating around the (vertical) pivot axis. Then, spinning of the wheel (around the wheelhub) is added. Imagine the gimbal axis to be locked, so that the wheel cannot pitch. The gimbal axis has sensors, that measure whether there is a torque around the gimbal axis.

In the picture, a section of the wheel has been named $dm 1$ . At the depicted moment in time, section $dm 1$ is at the perimeter of the rotating motion around the (vertical) pivot axis. Section $dm 1$ , therefore, has a lot of angular rotating velocity with respect to the rotation around the pivot axis, and as $dm 1$ is forced closer to the pivot axis of the rotation (by the wheel spinning further), because of the Coriolis effect, with respect to the vertical pivot axis, $dm 1$ tends to move in the direction of the top-left arrow in the diagram (shown at 45°) in the direction of rotation around the pivot axis.^[4] Section $dm 2$ of the wheel is moving away from the pivot axis, and so a force (again, a Coriolis force) acts in the same direction as in the case of $dm 1$ . Note that both arrows point in the same direction.

The same reasoning applies for the bottom half of the wheel, but there the arrows point in the opposite direction to that of the top arrows. Combined over the entire wheel, there is a torque around the gimbal axis when some spinning is added to rotation around a vertical axis.

It is important to note that the torque around the gimbal axis arises without any delay; the response is instantaneous.

In the discussion above, the setup was kept unchanging by preventing pitching around the gimbal axis. In the case of a spinning toy top, when the spinning top starts tilting, gravity exerts a torque. However, instead of rolling over, the spinning top just pitches a little. This pitching motion reorients the spinning top with respect to the torque that is being exerted. The result is that the torque exerted by gravity – via the pitching motion – elicits gyroscopic precession (which in turn yields a counter torque against the gravity torque) rather than causing the spinning top to fall to its side.

Precession or gyroscopic considerations have an effect on bicycle performance at high speed. Precession is also the mechanism behind gyrocompasses.

Classical (Newtonian)

The torque caused by the normal force - Fg and the weight of the top causes a change in the angular momentum L in the direction of that torque. This causes the top to precess. PrecessionOfATop.svg — The torque caused by the normal force – $F g$ and the weight of the top causes a change in the angular momentum $L$ in the direction of that torque. This causes the top to precess.

Precession is the change of angular velocity and angular momentum produced by a torque. The general equation that relates the torque to the rate of change of angular momentum is: ${\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}$ where ${\boldsymbol {\tau }}$ and $\mathbf {L}$ are the torque and angular momentum vectors respectively.

Due to the way the torque vectors are defined, it is a vector that is perpendicular to the plane of the forces that create it. Thus it may be seen that the angular momentum vector will change perpendicular to those forces. Depending on how the forces are created, they will often rotate with the angular momentum vector, and then circular precession is created.

Under these circumstances the angular velocity of precession is given by: ^[5]

{\boldsymbol {\omega }}_{\mathrm {p} }={\frac {\ mgr}{I_{\mathrm {s} }{\boldsymbol {\omega }}_{\mathrm {s} }}}={\frac {\tau }{I_{\mathrm {s} }{\boldsymbol {\omega }}_{\mathrm {s} }\sin(\theta )}}

where $I s$ is the moment of inertia, $ω s$ is the angular velocity of spin about the spin axis, $m$ is the mass, $g$ is the acceleration due to gravity, $θ$ is the angle between the spin axis and the axis of precession and $r$ is the distance between the center of mass and the pivot. The torque vector originates at the center of mass. Using $ω = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠2π/T⁠$ , we find that the period of precession is given by:^[6] $T_{\mathrm {p} }={\frac {4\pi ^{2}I_{\mathrm {s} }}{\ mgrT_{\mathrm {s} }}}={\frac {4\pi ^{2}I_{\mathrm {s} }\sin(\theta )}{\ \tau T_{\mathrm {s} }}}$

Where $I s$ is the moment of inertia, $T s$ is the period of spin about the spin axis, and $τ$ is the torque. In general, the problem is more complicated than this, however.

Relativistic (Einsteinian)

The special and general theories of relativity give three types of corrections to the Newtonian precession, of a gyroscope near a large mass such as Earth, described above. They are:

Thomas precession, a special-relativistic correction accounting for an object (such as a gyroscope) being accelerated along a curved path.
de Sitter precession, a general-relativistic correction accounting for the Schwarzschild metric of curved space near a large non-rotating mass.
Lense–Thirring precession, a general-relativistic correction accounting for the frame dragging by the Kerr metric of curved space near a large rotating mass.

The Schwarzschild geodesics (sometimes Schwarzschild precession) is used in the prediction of the anomalous perihelion precession of the planets, most notably for the accurate prediction of the apsidal precession of Mercury

Astronomy

In astronomy, precession refers to any of several gravity-induced, slow and continuous changes in an astronomical body's rotational axis or orbital path. Precession of the equinoxes, perihelion precession, changes in the tilt of Earth's axis to its orbit, and the eccentricity of its orbit over tens of thousands of years are all important parts of the astronomical theory of ice ages. (See Milankovitch cycles.)

Axial precession (precession of the equinoxes)

Axial precession is the movement of the rotational axis of an astronomical body, whereby the axis slowly traces out a cone. In the case of Earth, this type of precession is also known as the precession of the equinoxes, lunisolar precession, or precession of the equator. Earth goes through one such complete precessional cycle in a period of approximately 26,000 years or 1° every 72 years, during which the positions of stars will slowly change in both equatorial coordinates and ecliptic longitude. Over this cycle, Earth's north axial pole moves from where it is now, within 1° of Polaris, in a circle around the ecliptic pole, with an angular radius of about 23.5°.

The ancient Greek astronomer Hipparchus (c. 190–120 BC) is generally accepted to be the earliest known astronomer to recognize and assess the precession of the equinoxes at about 1° per century (which is not far from the actual value for antiquity, 1.38°),^[7] although there is some minor dispute about whether he was.^[8] In ancient China, the Jin-dynasty scholar-official Yu Xi (fl. 307–345 AD) made a similar discovery centuries later, noting that the position of the Sun during the winter solstice had drifted roughly one degree over the course of fifty years relative to the position of the stars.^[9] The precession of Earth's axis was later explained by Newtonian physics. Being an oblate spheroid, Earth has a non-spherical shape, bulging outward at the equator. The gravitational tidal forces of the Moon and Sun apply torque to the equator, attempting to pull the equatorial bulge into the plane of the ecliptic, but instead causing it to precess. The torque exerted by the planets, particularly Jupiter, also plays a role.^[10]

Precessional movement of the axis (left), precession of the equinox in relation to the distant stars (middle), and the path of the north celestial pole among the stars due to the precession. Vega is the bright star near the bottom (right).

Apsidal precession

The orbits of planets around the Sun do not really follow an identical ellipse each time, but actually trace out a flower-petal shape because the major axis of each planet's elliptical orbit also precesses within its orbital plane, partly in response to perturbations in the form of the changing gravitational forces exerted by other planets. This is called perihelion precession or apsidal precession.

In the adjunct image, Earth's apsidal precession is illustrated. As the Earth travels around the Sun, its elliptical orbit rotates gradually over time. The eccentricity of its ellipse and the precession rate of its orbit are exaggerated for visualization. Most orbits in the Solar System have a much smaller eccentricity and precess at a much slower rate, making them nearly circular and nearly stationary.

Discrepancies between the observed perihelion precession rate of the planet Mercury and that predicted by classical mechanics were prominent among the forms of experimental evidence leading to the acceptance of Einstein's Theory of Relativity (in particular, his General Theory of Relativity), which accurately predicted the anomalies.^[11]^[12] Deviating from Newton's law, Einstein's theory of gravitation predicts an extra term of $⁠ A / r 4 ⁠$ , which accurately gives the observed excess turning rate of 43 arcseconds every 100 years.

Nodal precession

Orbital nodes also precess over time.

Related Research Articles

<span class="mw-page-title-main">Angular momentum</span> Conserved physical quantity; rotational analogue of linear momentum

Angular momentum is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, flying discs, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it.

<span class="mw-page-title-main">Nutation</span> Wobble of the axis of rotation

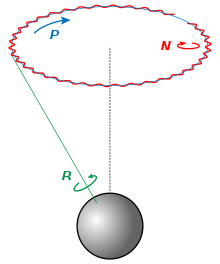
Nutation is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behaviour of a mechanism. In an appropriate reference frame it can be defined as a change in the second Euler angle. If it is not caused by forces external to the body, it is called free nutation or Euler nutation. A pure nutation is a movement of a rotational axis such that the first Euler angle is constant. Therefore it can be seen that the circular red arrow in the diagram indicates the combined effects of precession and nutation, while nutation in the absence of precession would only change the tilt from vertical. However, in spacecraft dynamics, precession is sometimes referred to as nutation.

<span class="mw-page-title-main">Torque</span> Turning force around an axis

In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force. The symbol for torque is typically $, the lowercase Greek letter tau . When being referred to as moment of force, it is commonly denoted by M . Just as a linear force is a push or a pull applied to a body, a torque can be thought of as a twist applied to an object with respect to a chosen point; for example, driving a screw uses torque, which is applied by the screwdriver rotating around its axis. A force of three newtons applied two metres from the fulcrum, for example, exerts the same torque as a force of one newton applied six metres from the fulcrum.$

A gyroscope is a device used for measuring or maintaining orientation and angular velocity. It is a spinning wheel or disc in which the axis of rotation is free to assume any orientation by itself. When rotating, the orientation of this axis is unaffected by tilting or rotation of the mounting, according to the conservation of angular momentum.

A gyrocompass is a type of non-magnetic compass which is based on a fast-spinning disc and the rotation of the Earth to find geographical direction automatically. A gyrocompass makes use of one of the seven fundamental ways to determine the heading of a vehicle. A gyroscope is an essential component of a gyrocompass, but they are different devices; a gyrocompass is built to use the effect of gyroscopic precession, which is a distinctive aspect of the general gyroscopic effect. Gyrocompasses, such as the fibre optic gyrocompass are widely used to provide a heading for navigation on ships. This is because they have two significant advantages over magnetic compasses:

<span class="mw-page-title-main">Angular velocity</span> Direction and rate of rotation

In physics, angular velocity, also known as angular frequency vector, is a pseudovector representation of how the angular position or orientation of an object changes with time, i.e. how quickly an object rotates around an axis of rotation and how fast the axis itself changes direction.

In physics, angular acceleration is the time rate of change of angular velocity. Following the two types of angular velocity, spin angular velocity and orbital angular velocity, the respective types of angular acceleration are: spin angular acceleration, involving a rigid body about an axis of rotation intersecting the body's centroid; and orbital angular acceleration, involving a point particle and an external axis.

<span class="mw-page-title-main">Moment of inertia</span> Scalar measure of the rotational inertia with respect to a fixed axis of rotation

The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relative to a rotational axis. It is the ratio between the torque applied and the resulting angular acceleration about that axis. It plays the same role in rotational motion as mass does in linear motion. A body's moment of inertia about a particular axis depends both on the mass and its distribution relative to the axis, increasing with mass & distance from the axis.

Rotational energy or angular kinetic energy is kinetic energy due to the rotation of an object and is part of its total kinetic energy. Looking at rotational energy separately around an object's axis of rotation, the following dependence on the object's moment of inertia is observed: $where$

In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass.

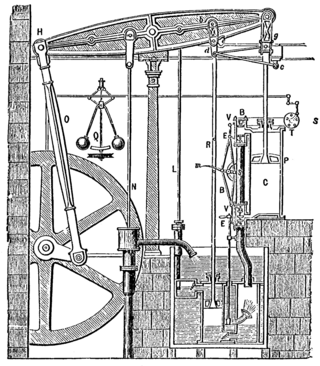
In the physical science of dynamics, rigid-body dynamics studies the movement of systems of interconnected bodies under the action of external forces. The assumption that the bodies are rigid simplifies analysis, by reducing the parameters that describe the configuration of the system to the translation and rotation of reference frames attached to each body. This excludes bodies that display fluid, highly elastic, and plastic behavior.

In classical mechanics, Euler's rotation equations are a vectorial quasilinear first-order ordinary differential equation describing the rotation of a rigid body, using a rotating reference frame with angular velocity ω whose axes are fixed to the body. Their general vector form is

In physics, the gyromagnetic ratio of a particle or system is the ratio of its magnetic moment to its angular momentum, and it is often denoted by the symbol $γ$ , gamma. Its SI unit is the radian per second per tesla (rad⋅s⁻¹⋅T⁻¹) or, equivalently, the coulomb per kilogram (C⋅kg⁻¹).

In physics, the Thomas precession, named after Llewellyn Thomas, is a relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular velocity of the orbital motion.

<span class="mw-page-title-main">Rotation around a fixed axis</span> Type of motion

Rotation around a fixed axis or axial rotation is a special case of rotational motion around an axis of rotation fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis of rotation changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will result.

In classical mechanics, Poinsot's construction is a geometrical method for visualizing the torque-free motion of a rotating rigid body, that is, the motion of a rigid body on which no external forces are acting. This motion has four constants: the kinetic energy of the body and the three components of the angular momentum, expressed with respect to an inertial laboratory frame. The angular velocity vector $of the rigid rotor is not constant, but satisfies Euler's equations. The conservation of kinetic energy and angular momentum provide two constraints on the motion of .$

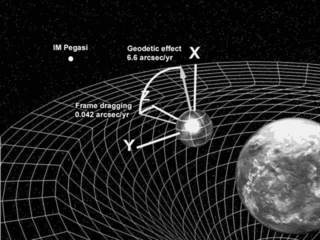
The geodetic effect represents the effect of the curvature of spacetime, predicted by general relativity, on a vector carried along with an orbiting body. For example, the vector could be the angular momentum of a gyroscope orbiting the Earth, as carried out by the Gravity Probe B experiment. The geodetic effect was first predicted by Willem de Sitter in 1916, who provided relativistic corrections to the Earth–Moon system's motion. De Sitter's work was extended in 1918 by Jan Schouten and in 1920 by Adriaan Fokker. It can also be applied to a particular secular precession of astronomical orbits, equivalent to the rotation of the Laplace–Runge–Lenz vector.

In general relativity, Lense–Thirring precession or the Lense–Thirring effect is a relativistic correction to the precession of a gyroscope near a large rotating mass such as the Earth. It is a gravitomagnetic frame-dragging effect. It is a prediction of general relativity consisting of secular precessions of the longitude of the ascending node and the argument of pericenter of a test particle freely orbiting a central spinning mass endowed with angular momentum $.$

<span class="mw-page-title-main">Gyroscopic exercise tool</span>

A gyroscopic exercise tool is a specialized device used in physical therapy to improve wrist strength and promote the development of palm, wrist, forearm, and finger muscles. It can also be used as a unique demonstration of some aspects of rotational dynamics. The device consists of a tennis ball-sized plastic or metal shell surrounding a free-spinning mass, with an inner heavy core, which can be spun by a short rip string or using a self-start mechanism by means of rewinding it against a spring to give it potential energy. Once the gyroscope inside is going fast enough, the person holding the device can accelerate the spinning mass to high rotation rates by moving the wrist in a circular motion. The force enacted on the user increases as the speed of the inner gyroscope increases.

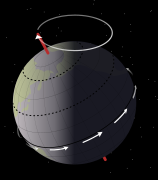
Nodal precession is the precession of the orbital plane of a satellite around the rotational axis of an astronomical body such as Earth. This precession is due to the non-spherical nature of a rotating body, which creates a non-uniform gravitational field. The following discussion relates to low Earth orbit of artificial satellites, which have no measurable effect on the motion of Earth. The nodal precession of more massive, natural satellites like the Moon is more complex.

References

↑ Schaub, Hanspeter (2003), Analytical Mechanics of Space Systems, AIAA, pp. 149–150, ISBN 9781600860270
↑ Boal, David (2001). "Lecture 26 – Torque-free rotation – body-fixed axes" (PDF). Retrieved 2008-09-17.
↑ Sharma, Ishan; Burns, Joseph A.; Hui, C.-H. (2005). "Nutational damping times in solids of revolution". Monthly Notices of the Royal Astronomical Society. 359 (1): 79. Bibcode:2005MNRAS.359...79S. doi: 10.1111/j.1365-2966.2005.08864.x .
↑ Teodorescu, Petre P (2002). Mechanical Systems, Classical Models: Volume II: Mechanics of Discrete and Continuous Systems. Springer Science & Business Media. p. 420. ISBN 978-1-4020-8988-6.
↑ Moebs, William; Ling, Samuel J.; Sanny, Jeff (Sep 19, 2016). 11.4 Precession of a Gyroscope - University Physics Volume 1 | OpenStax. Houston, Texas. Retrieved 23 October 2020.{{cite book}}: CS1 maint: location missing publisher (link)
↑ Moebs, William; Ling, Samuel J.; Sanny, Jeff (Sep 19, 2016). 11.4 Precession of a Gyroscope - University Physics Volume 1 | OpenStax. Houston, Texas. Retrieved 23 October 2020.{{cite book}}: CS1 maint: location missing publisher (link)
↑ Barbieri, Cesare (2007). Fundamentals of Astronomy. New York: Taylor and Francis Group. p. 71. ISBN 978-0-7503-0886-1.
↑ Swerdlow, Noel (1991). On the cosmical mysteries of Mithras. Classical Philology, 86, (1991), 48–63. p. 59.
↑ Sun, Kwok. (2017). Our Place in the Universe: Understanding Fundamental Astronomy from Ancient Discoveries, second edition. Cham, Switzerland: Springer. ISBN 978-3-319-54171-6, p. 120; see also Needham, Joseph; Wang, Ling. (1995) [1959]. Science and Civilization in China: Mathematics and the Sciences of the Heavens and the Earth, vol. 3, reprint edition. Cambridge: Cambridge University Press. ISBN 0-521-05801-5, p. 220.
↑ Bradt, Hale (2007). Astronomy Methods. Cambridge University Press. p. 66. ISBN 978-0-521-53551-9.
↑ Max Born (1924), Einstein's Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and Earth.)
↑ "An even larger value for a precession has been found, for a black hole in orbit around a much more massive black hole, amounting to 39 degrees each orbit". 18 March 2008. Archived from the original on 2018-08-07. Retrieved 2023-11-15.{{cite web}}: CS1 maint: bot: original URL status unknown (link)

External links

Media related to Precession at Wikimedia Commons
Explanation and derivation of formula for precession of a top
Precession and the Milankovich theory From Stargazers to Starships

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Schaub, Hanspeter (2003), Analytical Mechanics of Space Systems, AIAA, pp. 149–150, ISBN 9781600860270

[2] Boal, David (2001). "Lecture 26 – Torque-free rotation – body-fixed axes" (PDF). Retrieved 2008-09-17.

[3] Sharma, Ishan; Burns, Joseph A.; Hui, C.-H. (2005). "Nutational damping times in solids of revolution". Monthly Notices of the Royal Astronomical Society. 359 (1): 79. Bibcode:2005MNRAS.359...79S. doi: 10.1111/j.1365-2966.2005.08864.x .

[Teodorescu-4] Teodorescu, Petre P (2002). Mechanical Systems, Classical Models: Volume II: Mechanics of Discrete and Continuous Systems. Springer Science & Business Media. p. 420. ISBN 978-1-4020-8988-6.

[5] Moebs, William; Ling, Samuel J.; Sanny, Jeff (Sep 19, 2016). 11.4 Precession of a Gyroscope - University Physics Volume 1 | OpenStax. Houston, Texas. Retrieved 23 October 2020.{{cite book}}: CS1 maint: location missing publisher (link)

[6] Moebs, William; Ling, Samuel J.; Sanny, Jeff (Sep 19, 2016). 11.4 Precession of a Gyroscope - University Physics Volume 1 | OpenStax. Houston, Texas. Retrieved 23 October 2020.{{cite book}}: CS1 maint: location missing publisher (link)

[7] Barbieri, Cesare (2007). Fundamentals of Astronomy. New York: Taylor and Francis Group. p. 71. ISBN 978-0-7503-0886-1.

[8] Swerdlow, Noel (1991). On the cosmical mysteries of Mithras. Classical Philology, 86, (1991), 48–63. p. 59.

[9] Sun, Kwok. (2017). Our Place in the Universe: Understanding Fundamental Astronomy from Ancient Discoveries, second edition. Cham, Switzerland: Springer. ISBN 978-3-319-54171-6, p. 120; see also Needham, Joseph; Wang, Ling. (1995) [1959]. Science and Civilization in China: Mathematics and the Sciences of the Heavens and the Earth, vol. 3, reprint edition. Cambridge: Cambridge University Press. ISBN 0-521-05801-5, p. 220.

[Bradt-10] Bradt, Hale (2007). Astronomy Methods. Cambridge University Press. p. 66. ISBN 978-0-521-53551-9.

[11] Max Born (1924), Einstein's Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and Earth.)

[12] "An even larger value for a precession has been found, for a black hole in orbit around a much more massive black hole, amounting to 39 degrees each orbit". 18 March 2008. Archived from the original on 2018-08-07. Retrieved 2023-11-15.{{cite web}}: CS1 maint: bot: original URL status unknown (link)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]