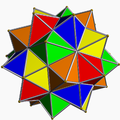
Compound of five tetrahemihexahedra

Compound of five tetrahemihexahedra
Type	Uniform compound
Index	UC18
Polyhedra	5 tetrahemihexahedra
Faces	20 triangles, 15 squares
Edges	60
Vertices	30
Symmetry group	chiral icosahedral (I)
Subgroup restricting to one constituent	chiral tetrahedral (T)

A compound of five tetrahemihexahedra is a uniform polyhedron compound and a symmetric arrangement of five tetrahemihexahedra. It could be also called a hemirhombichiricosahedron. It is chiral with icosahedral symmetry (I).

Related polyhedra

Five tetrahemihexahedra in an icosidodecahedron

Its convex hull is an icosidodecahedron. Hence it is a faceting of an icosidodecahedron, shown at left. It shares its edges and triangular faces with the compound of five octahedra.

Icosidodecahedron

Compound of five octahedra

Compound of five tetrahemihexahedra

See also

• Compound of twenty tetrahemihexahedra

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, doi:10.1017/S0305004100052440, MR   0397554 .
• McCooey, Robert. "Uniform Polyhedron Compounds". Hedron Dude. Retrieved 24 June 2025.