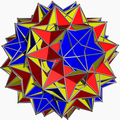
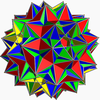
Compound of twenty tetrahemihexahedra

Compound of twenty tetrahemihexahedra
Type	Uniform compound
Index	UC19
Polyhedra	20 tetrahemihexahedra
Faces	20+60 triangles, 60 squares
Edges	240
Vertices	60
Symmetry group	chiral icosahedral (I)
Subgroup restricting to one constituent	3-fold rotational (C3)

This uniform polyhedron compound is a symmetric arrangement of 20 tetrahemihexahedra. It is chiral with icosahedral symmetry (I).

John Skilling notes, in his enumeration of uniform compounds of uniform polyhedra, that this compound of 20 tetrahemihexahedra is unique in that it cannot be obtained by "adding symmetry to a group in which the basic polyhedron is uniform". Each tetrahemihexahedron in this compound is embedded with symmetry group C₃, which does not act transitively over the tetrahemihexahedron's six vertices. However, the compound as a whole can achieve uniformity because two tetrahemihexahedra coincide at each vertex.

Related polyhedra

This compound shares its edge arrangement with the great dirhombicosidodecahedron, the great disnub dirhombidodecahedron, and the compound of 20 octahedra.

The edges and 20 of the triangular faces occur in one enantiomer of the great snub dodecicosidodecahedron, with the other 60 triangular faces occurring in the other enantiomer.

Convex hull (Nonuniform rhombicosidodecahedron)	Great snub dodecicosidodecahedron	Great dirhombicosidodecahedron
Great disnub dirhombidodecahedron	Compound of twenty octahedra	Compound of twenty tetrahemihexahedra

See also

• Compound of five tetrahemihexahedra

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, Bibcode:1976MPCPS..79..447S, doi:10.1017/S0305004100052440, MR   0397554, S2CID   123279687 .