Compound of twenty octahedra

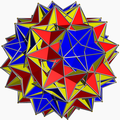
Compound of twenty octahedra
Type	Uniform compound
Index	UC14
Polyhedra	20 octahedra
Faces	40+120 triangles
Edges	240
Vertices	60
Symmetry group	icosahedral (Ih)
Subgroup restricting to one constituent	6-fold improper rotation (S6)

3D model of a compound of twenty octahedra

The compound of twenty octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra (considered as triangular antiprisms). It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide.

Related polyhedra

This compound shares its edge arrangement with the great dirhombicosidodecahedron, the great disnub dirhombidodecahedron, and the compound of twenty tetrahemihexahedra.

It may be constructed as the exclusive or of the two enantiomorphs of the great snub dodecicosidodecahedron.

Convex hull (Non-uniform Rhombicosidodecahedron)	Great snub dodecicosidodecahedron	Great dirhombicosidodecahedron
Great disnub dirhombidodecahedron	Compound of twenty octahedra	Compound of twenty tetrahemihexahedra

See also

• Compound of three octahedra
• Compound of four octahedra
• Compound of five octahedra
• Compound of ten octahedra

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, doi:10.1017/S0305004100052440, MR   0397554 .