Compound of three octahedra

Last updated
Compound of three octahedra
Compound of three octahedra.svg
Polyhedra3 regular octahedra
Faces24 equilateral triangles
Edges36
Vertices18
Symmetry group
(Single color)		 Oh, order 48

In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized by M. C. Escher, who used it in the central image of his 1948 woodcut Stars .

Contents

Construction

A regular octahedron can be circumscribed around a cube in such a way that the eight edges of two opposite squares of the cube lie on the eight faces of the octahedron. The three octahedra formed in this way from the three pairs of opposite cube squares form the compound of three octahedra. [1] The eight cube vertices are the same as the eight points in the compound where three edges cross each other. [2] Each of the octahedron edges that participates in these triple crossings is divided by the crossing point in the ratio 1:√2. [2] The remaining octahedron edges cross each other in pairs, within the interior of the compound; their crossings are at their midpoints and form right angles.

The compound of three octahedra can also be formed from three copies of a single octahedron by rotating each copy by an angle of π/4 around one of the three symmetry axes that pass through two opposite vertices of the starting octahedron. [3] A third construction for the same compound of three octahedra is as the dual polyhedron of the compound of three cubes, one of the uniform polyhedron compounds.

The six vertices of one of the three octahedra may be given by the coordinates (0, 0, ±2) and (±√2, ±√2, 0). The other two octahedra have coordinates that may be obtained from these coordinates by exchanging the z coordinate for the x or y coordinate. [1] [2]

Symmetries

The stellated rhombic dodecahedron, a compound of three flattened octahedra used in Escher's Study for Stars and Waterfall. Three flattened octahedra compound.png
The stellated rhombic dodecahedron, a compound of three flattened octahedra used in Escher's Study for Stars and Waterfall .

The compound of three octahedra has the same symmetry group as a single octahedron. It is an isohedral deltahedron, meaning that its faces are equilateral triangles and that it has a symmetry taking every face to every other face. There is one known infinite family of isohedral deltahedra, and 36 more that do not fall into this family; the compound of three octahedra is one of the 36 sporadic examples. [4] However, its symmetry group does not take every vertex to every other vertex, so it is not itself a uniform polyhedron compound.

The intersection of the three octahedra is a convex polyhedron with 14 vertices and 24 faces, a tetrakis hexahedron, formed by attaching a low square pyramid to each face of the central cube. [2] Thus, the compound can be seen as a stellation of the tetrakis hexahedron. A different form of the tetrakis hexahedron, formed by using taller pyramids on each face of the cube, is non-convex but has equilateral triangle faces that again lie on the same planes as the faces of the three octahedra; it is another of the known isohedral deltahedra. A third isohedral deltahedron sharing the same face planes, the compound of six tetrahedra, may be formed by stellating each face of the compound of three octahedra to form three stellae octangulae. A fourth isohedral deltahedron with the same face planes, also a stellation of the compound of three octahedra, has the same combinatorial structure as the tetrakis hexahedron but with the cube faces dented inwards into intersecting pyramids rather than attaching the pyramids to the exterior of the cube. [4]

The cube around which the three octahedra can be circumscribed has nine planes of reflection symmetry. Three of these reflection panes pass parallel to the sides of the cube, halfway between two opposite sides; the other six pass diagonally across the cube, through four of its vertices. These nine planes coincide with the nine equatorial planes of the three octahedra. [2]

History

Octahedron circumscribed around a cube, as drawn by Piero della Francesca for his book De quinque corporibus regularibus Piero della Francesca - Libellus de quinque corporibus regularibus - p41b (cropped).jpg
Octahedron circumscribed around a cube, as drawn by Piero della Francesca for his book De quinque corporibus regularibus

In the 15th-century manuscript De quinque corporibus regularibus by Piero della Francesca, della Francesca already includes a drawing of an octahedron circumscribed around a cube, with eight of the cube edges lying in the octahedron's eight faces. Three octahedra circumscribed in this way around a single cube would form the compound of three octahedra, but della Francesca does not depict the compound. [5]

The next appearance of the compound of three octahedra in the mathematical literature appears to be a 1900 work by Max Brückner, which mentions it and includes a photograph of a model of it. [2] [6]

Dutch artist M. C. Escher, in his 1948 woodcut Stars , used as the central figure of the woodcut a cage in this shape, containing two chameleons and floating through space. [7] H. S. M. Coxeter, assuming that Escher rediscovered this shape independently, writes that "It is remarkable that Escher, without any knowledge of algebra or analytic geometry, was able to rediscover this highly symmetrical figure." [2] However, George W. Hart has documented that Escher was familiar with Brückner's work and used it as the basis for many of the stellated polyhedra and polyhedral compounds that he drew. [8] Earlier in 1948, Escher had made a preliminary woodcut with a similar theme, Study for Stars, but instead of using the compound of three regular octahedra in the study he used a different but related shape, a stellated rhombic dodecahedron (sometimes called Escher's solid), which can be formed as a compound of three flattened octahedra. [9] This form as a polyhedron is topologically identical to the disdyakis dodecahedron, which can be seen as rhombic dodecahedron with shorter pyramids on the rhombic faces. The dual figure of the octahedral compound, the compound of three cubes, is also shown in a later Escher woodcut, Waterfall , next to the same stellated rhombic dodecahedron. [7]

The compound of three octahedra re-entered the mathematical literature more properly with the work of Bakos & Johnson (1959), who observed its existence and provided coordinates for its vertices. It was studied in more detail by Wenninger (1968) and Coxeter (1985).

Other compounds of three octahedra

With the octahedra seen as triangular antiprisms, another uniform prismatic compound of antiprisms exists with D3d symmetry, order 12. Each antiprism is rotated 40 degrees. The top and bottom planes can be seen to contain the compound enneagram, {9/3} or 3{3}.

Compound three triangular antiprisms.png

See also

Related Research Articles

Cuboctahedron Polyhedron with 8 triangular faces and 6 square faces

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

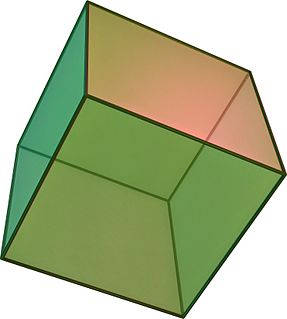
Cube A geometric 3-dimensional object with 6 square faces

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.

Regular icosahedron One of the five Platonic solids

In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.

Octahedron Polyhedron with 8 triangular faces

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

A polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.

A Platonic solid is a convex regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:

Rhombicuboctahedron Archimedean solid with eight triangular, six square, and twelve rectangular faces

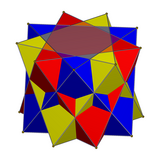
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

Stellation Extending the elements of a polytope to form a new figure

In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from Latin stella, "star". Stellation is the reciprocal or dual process to faceting.

Rhombic dodecahedron

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.

Tetrakis hexahedron Polyhedron

In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.

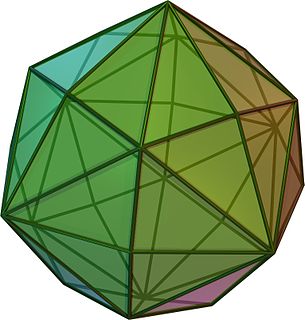
Disdyakis dodecahedron Geometric shape with 48 faces

In geometry, a disdyakis dodecahedron,, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it. More formally, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron. The net of the rhombic dodecahedral pyramid also shares the same topology.

<i>Stars</i> (M. C. Escher) Wood engraving print by M. C. Escher

Stars is a wood engraving print created by the Dutch artist M. C. Escher in 1948, depicting two chameleons in a polyhedral cage floating through space.

Uniform polyhedron Class of mathematical solids

A uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.

In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive.

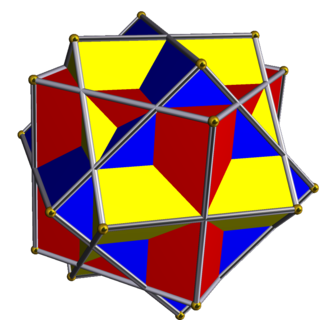
Compound of three cubes Polyhedral compound

In geometry, the compound of three cubes is a uniform polyhedron compound formed from three cubes arranged with octahedral symmetry. It has been depicted in works by Max Brückner and M.C. Escher.

Tetrakis cuboctahedron

The tetrakis cuboctahedron is a convex polyhedron with 32 triangular faces, 48 edges, and 18 vertices. It is a dual of the truncated rhombic dodecahedron.

First stellation of the rhombic dodecahedron

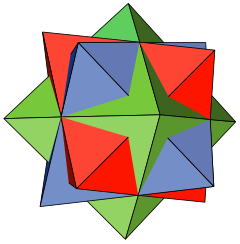
In geometry, the first stellation of the rhombic dodecahedron is a self-intersecting polyhedron with 12 faces, each of which is a non-convex hexagon. It is a stellation of the rhombic dodecahedron and has the same outer shell and the same visual appearance as two other shapes: a solid, Escher's solid, with 48 triangular faces, and a polyhedral compound of three flattened octahedra with 24 overlapping triangular faces.

Chamfer (geometry)

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.

Icosahedron Polyhedron with 20 faces

In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty' and from Ancient Greek ἕδρα (hédra) ' seat'. The plural can be either "icosahedra" or "icosahedrons".

References

  1. 1 2 Bakos, T.; Johnson, Norman W. (1959), "Octahedra inscribed in a cube", The Mathematical Gazette, 43 (343): 17–20, JSTOR   3608867 .
  2. 1 2 3 4 5 6 7 Coxeter, H. S. M. (1985), "A special book review: M. C. Escher: His life and complete graphic work", The Mathematical Intelligencer, 7 (1): 59–69, doi:10.1007/BF03023010 . The discussion of the compound of three octahedra is on pp. 61–62.
  3. ↑ Wenninger, M. J. (1968), "Some interesting octahedral compounds", The Mathematical Gazette, 52 (379): 16–23, JSTOR   3614454 .
  4. 1 2 Shephard, G. C. (1999), "Isohedral deltahedra", Periodica Mathematica Hungarica, 39 (1–3): 83–106, doi:10.1023/A:1004838806529 .
  5. ↑ Hart, George W. (1998), "Piero della Francesca's Polyhedra", Virtual Polyhedra .
  6. ↑ Brückner, Max (1900), Vielecke und Vielflache, Leipzig: Teubner, p. 188 and Tafel VIII 12. As cited by Coxeter (1985).
  7. 1 2 Hart, George W. (1996), "The Polyhedra of M.C. Escher", Virtual Polyhedra .
  8. ↑ Hart, George W., "Max Brücknerʼs Wunderkammer of Paper Polyhedra", Bridges 2019 Conference Proceedings (PDF), pp. 59–66
  9. ↑ The compound of three octahedra and a remarkable compound of three square dipyramids, the Escher's solid, Livio Zefiro, University of Genova.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.