In geometry, an octahedron is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
20 (twenty) is the natural number following 19 and preceding 21.

In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876.

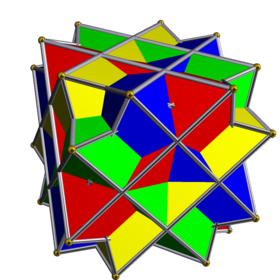
The compound of twenty octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra. It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide.
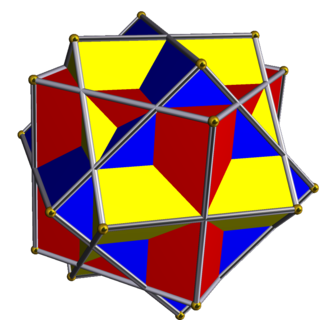
In geometry, the compound of three cubes is a uniform polyhedron compound formed from three cubes arranged with octahedral symmetry. It has been depicted in works by Max Brückner and M.C. Escher.
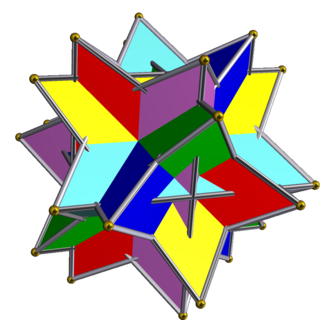
The compound of six tetrahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 6 tetrahedra. It can be constructed by inscribing a stella octangula within each cube in the compound of three cubes, or by stellating each octahedron in the compound of three octahedra.
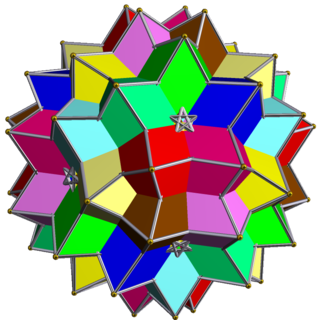
The compounds of ten octahedra UC15 and UC16 are two uniform polyhedron compounds. They are composed of a symmetric arrangement of 10 octahedra, considered as triangular antiprisms, aligned with the axes of three-fold rotational symmetry of an icosahedron. The two compounds differ in the orientation of their octahedra: each compound may be transformed into the other by rotating each octahedron by 60 degrees.

The compound of eight octahedra with rotational freedom is a uniform polyhedron compound. It is composed of a symmetric arrangement of 8 octahedra, considered as triangular antiprisms. It can be constructed by superimposing eight identical octahedra, and then rotating them in pairs about the four axes that pass through the centres of two opposite octahedral faces. Each octahedron is rotated by an equal angle θ.
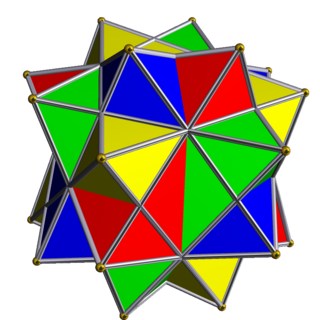
The compound of four octahedra with rotational freedom is a uniform polyhedron compound. It consists in a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by an equal angle θ about a separate axis passing through the centres of two opposite octahedral faces, in such a way as to preserve pyritohedral symmetry.

The compound of twenty octahedra with rotational freedom is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra, considered as triangular antiprisms. It can be constructed by superimposing two copies of the compound of 10 octahedra UC16, and for each resulting pair of octahedra, rotating each octahedron in the pair by an equal and opposite angle θ.

In hyperbolic geometry, a uniform honeycomb in hyperbolic space is a uniform tessellation of uniform polyhedral cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by permutations of rings of the Coxeter diagrams for each family.
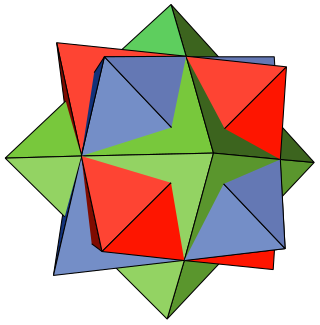
In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized by M. C. Escher, who used it in the central image of his 1948 woodcut Stars.

The compound of four cubes or Bakos compound is a face-transitive polyhedron compound of four cubes with octahedral symmetry. It is the dual of the compound of four octahedra. Its surface area is 687/77 square lengths of the edge.
The compound of six octahedra has two forms. One form is a symmetric arrangement of 6 octahedra, considered as square bipyramid. It is a dual of a special case of the compound of 6 cubes with rotational freedom.