| Compound of six pentagonal prisms | |
|---|---|
 | |
| Type | Uniform compound |
| Index | UC34 |
| Polyhedra | 6 pentagonal prisms |
| Faces | 12 pentagons, 30 squares |
| Edges | 90 |
| Vertices | 60 |
| Symmetry group | chiral icosahedral (I) |
| Subgroup restricting to one constituent | 5-fold dihedral (D5) |
This uniform polyhedron compound is a chiral symmetric arrangement of six pentagonal prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.
This compound shares its vertex arrangement with four uniform polyhedra as follows:
 Nonconvex great rhombicosidodecahedron |  Great dodecicosidodecahedron |  Great rhombidodecahedron |
 Truncated great dodecahedron |  Compound of six pentagonal prisms |  Compound of twelve pentagonal prisms |
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876.
In geometry, a uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform, i.e. the symmetry group of the compound acts transitively on the compound's vertices.
This uniform polyhedron compound is a symmetric arrangement of 20 tetrahemihexahedra. It is chiral with icosahedral symmetry (I).
The compound of twenty octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra. It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide.
This uniform polyhedron compound is a composition of 5 cubohemioctahedra, in the same arrangement as in the compound of 5 cuboctahedra.
In geometry, this uniform polyhedron compound is a composition of 5 octahemioctahedra, in the same vertex arrangement as in the compound of 5 cuboctahedra.
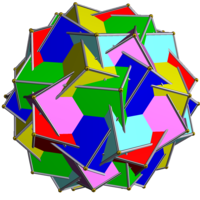
This uniform polyhedron compound is a composition of 5 rhombicuboctahedra, in the same vertex arrangement the compound of 5 stellated truncated hexahedra.
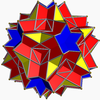
This uniform polyhedron compound is a composition of 5 nonconvex great rhombicuboctahedra, in the same arrangement the compound of 5 truncated cubes.
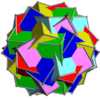
This uniform polyhedron compound is a composition of 5 great cubicuboctahedra, in the same arrangement as the compound of 5 truncated cubes.
This uniform polyhedron compound is a composition of 5 great rhombihexahedra, in the same vertex arrangement as the compound of 5 truncated cubes.
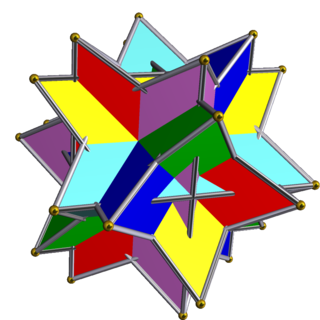
The compound of six tetrahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 6 tetrahedra. It can be constructed by inscribing a stella octangula within each cube in the compound of three cubes, or by stellating each octahedron in the compound of three octahedra.
This uniform polyhedron compound is a chiral symmetric arrangement of 10 triangular prisms, aligned with the axes of three-fold rotational symmetry of an icosahedron.
This uniform polyhedron compound is a symmetric arrangement of 20 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an icosahedron.
This uniform polyhedron compound is a symmetric arrangement of 8 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an octahedron. It results from composing the two enantiomorphs of the compound of 4 triangular prisms.
The compound of four octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis.
This uniform polyhedron compound is a chiral symmetric arrangement of 6 pentagrammic prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.
This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.
This uniform polyhedron compound is a symmetric arrangement of 12 pentagonal prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |