The compound of small stellated dodecahedron and great dodecahedron is a polyhedron compound where the great dodecahedron is internal to its dual, the small stellated dodecahedron.
This can be seen as one of the two three-dimensional equivalents of the compound of two pentagrams ({10/4} "decagram"); this series continues into the fourth dimension as compounds of star 4-polytopes.
In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra.
In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from Latin stella, "star". Stellation is the reciprocal or dual process to faceting.
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces, intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex.
In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.
In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.
In geometry, the great icosahedron is one of four Kepler-Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.
In geometry, a compound of two tetrahedra is constructed by two overlapping tetrahedra, usually implied as regular tetrahedra.
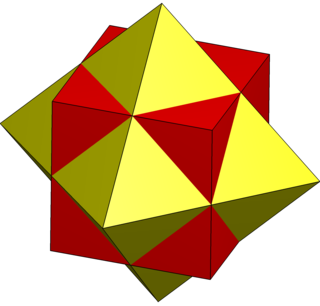
The compound of cube and octahedron is a polyhedron which can be seen as either a polyhedral stellation or a compound.
In geometry, this polyhedron can be seen as either a polyhedral stellation or a compound.
There are two different compounds of great icosahedron and great stellated dodecahedron: one is a dual compound and a stellation of the great icosidodecahedron, the other is a stellation of the icosidodecahedron.
In geometry, the great grand stellated 120-cell or great grand stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol {5/2,3,3}, one of 10 regular Schläfli-Hess 4-polytopes. It is unique among the 10 for having 600 vertices, and has the same vertex arrangement as the regular convex 120-cell.
In geometry, the grand 600-cell or grand polytetrahedron is a regular star 4-polytope with Schläfli symbol {3,3,5/2}. It is one of 10 regular Schläfli-Hess polytopes. It is the only one with 600 cells.
In geometry, the icosahedral 120-cell, polyicosahedron, faceted 600-cell or icosaplex is a regular star 4-polytope with Schläfli symbol {3,5,5/2}. It is one of 10 regular Schläfli-Hess polytopes.
In geometry, faceting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.
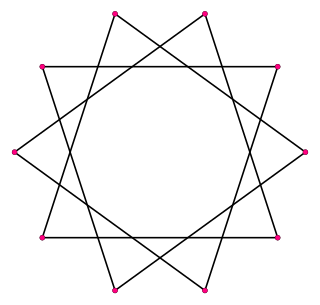
In geometry, a decagram is a 10-point star polygon. There is one regular decagram, containing the vertices of a regular decagon, but connected by every third point. Its Schläfli symbol is {10/3}.
In geometry, the medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is a stellation of the rhombic triacontahedron, and can also be called small stellated triacontahedron. Its dual is the dodecadodecahedron.
In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces, 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron.
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |
