| Compound of ten triangular prisms | |
|---|---|
 | |
| Type | Uniform compound |
| Index | UC32 |
| Polyhedra | 10 triangular prisms |
| Faces | 20 triangles, 30 squares |
| Edges | 90 |
| Vertices | 60 |
| Symmetry group | chiral icosahedral (I) |
| Subgroup restricting to one constituent | 3-fold dihedral (D3) |
This uniform polyhedron compound is a chiral symmetric arrangement of 10 triangular prisms, aligned with the axes of three-fold rotational symmetry of an icosahedron.
This compound shares its vertex arrangement with three uniform polyhedra as follows:
 convex hull |  Rhombidodecadodecahedron |  Icosidodecadodecahedron |
 Rhombicosahedron |  Compound of ten triangular prisms |  Compound of twenty triangular prisms |
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
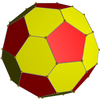
In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
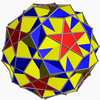
In geometry, the great dodecahedron is one of four Kepler–Poinsot polyhedra. It is composed of 12 pentagonal faces, intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex.
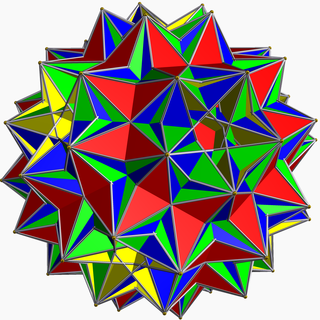
In geometry, the great disnub dirhombidodecahedron, also called Skilling's figure, is a degenerate uniform star polyhedron.
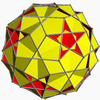
In geometry, the truncated great dodecahedron is a nonconvex uniform polyhedron, indexed as U37. It has 24 faces (12 pentagrams and 12 decagons), 90 edges, and 60 vertices. It is given a Schläfli symbol t{5,5/2}.
In geometry, the small stellated truncated dodecahedron (or quasitruncated small stellated dodecahedron or small stellatruncated dodecahedron) is a nonconvex uniform polyhedron, indexed as U58. It has 24 faces (12 pentagons and 12 decagrams), 90 edges, and 60 vertices. It is given a Schläfli symbol t{5⁄3,5}, and Coxeter diagram .
The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876.
In geometry, a uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform, i.e. the symmetry group of the compound acts transitively on the compound's vertices.
This uniform polyhedron compound is a symmetric arrangement of 20 tetrahemihexahedra. It is chiral with icosahedral symmetry (I).
The compound of twenty octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra. It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide.
This uniform polyhedron compound is a composition of 5 great rhombihexahedra, in the same vertex arrangement as the compound of 5 truncated cubes.
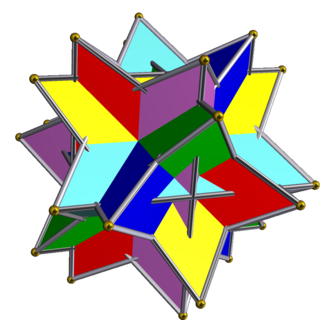
The compound of six tetrahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 6 tetrahedra. It can be constructed by inscribing a stella octangula within each cube in the compound of three cubes, or by stellating each octahedron in the compound of three octahedra.
This uniform polyhedron compound is a symmetric arrangement of 20 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an icosahedron.
The compound of four octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis.
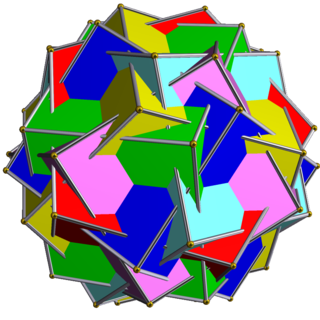
This uniform polyhedron compound is a chiral symmetric arrangement of six pentagonal prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.
This uniform polyhedron compound is a chiral symmetric arrangement of 6 pentagrammic prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.
This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.
This uniform polyhedron compound is a symmetric arrangement of 12 pentagonal prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.
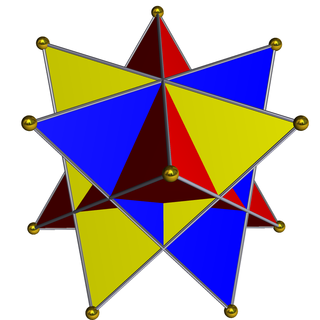
In geometry, a compound of three tetrahedra can be constructed by three tetrahedra rotated by 60 degree turns along an axis of the middle of an edge. It has dihedral symmetry, D3d, order 12. It is a uniform prismatic compound of antiprisms, UC23.
In geometry, a dodecagram is a star polygon or compound with 12 vertices. There is one regular dodecagram polygon. There are also 4 regular compounds {12/2},{12/3},{12/4}, and {12/6}.
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |