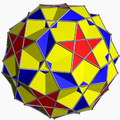
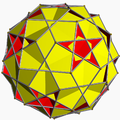
Compound of twenty triangular prisms

Compound of twenty triangular prisms
Type	Uniform compound
Index	UC33
Polyhedra	20 triangular prisms
Faces	40 triangles, 60 squares
Edges	180
Vertices	60
Symmetry group	icosahedral (Ih)
Subgroup restricting to one constituent	3-fold dihedral (D3)

This uniform polyhedron compound is a symmetric arrangement of 20 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an icosahedron.

It results from composing the two enantiomorphs of the compound of 10 triangular prisms. In doing so, the vertices of the two enantiomorphs coincide, with the result that the full compound has two triangular prisms incident on each of its vertices.

Related polyhedra

This compound shares its vertex arrangement with three uniform polyhedra as follows:

convex hull	Rhombidodecadodecahedron	Icosidodecadodecahedron
Rhombicosahedron	Compound of ten triangular prisms	Compound of twenty triangular prisms

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, doi:10.1017/S0305004100052440, MR   0397554 .