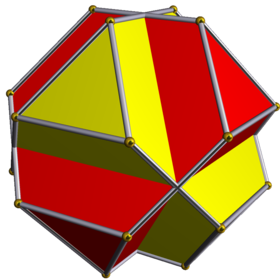
| Compound of two truncated tetrahedra | |
|---|---|
 | |
| Type | Uniform compound |
| Index | UC54 |
| Schläfli symbol | a2{4,3} |
| Coxeter diagram |    +  =     |
| Polyhedra | 2 truncated tetrahedra |
| Faces | 8 triangles 8 hexagons |
| Edges | 36 |
| Vertices | 24 |
| Symmetry group | octahedral (Oh) [4,3] |
| Subgroup restricting to one constituent | tetrahedral (Td) [3,3] |
This uniform polyhedron compound is a composition of two truncated tetrahedra, formed by truncating each of the tetrahedra in the stellated octahedron. It is related to the cantic cube construction of the truncated tetrahedron, as 
, which is one of the two dual positions represented in this compound.
The vertex arrangement is the same as a convex, but nonuniform rhombicuboctahedron having 12 rectangular faces.
