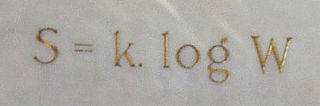In statistical mechanics and mathematics, a Boltzmann distribution is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. The distribution is expressed in the form:

Entropy is a scientific concept as well as a measurable physical property that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication.

In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable , which takes values in the alphabet and is distributed according to :

The Boltzmann constant is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, and in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating thermal noise in resistors. The Boltzmann constant has dimensions of energy divided by temperature, the same as entropy. It is named after the Austrian scientist Ludwig Boltzmann.
In physics, specifically statistical mechanics, an ensemble is an idealization consisting of a large number of virtual copies of a system, considered all at once, each of which represents a possible state that the real system might be in. In other words, a statistical ensemble is set of systems of particles used in statistical mechanics to describe a single system. The concept of an ensemble was introduced by J. Willard Gibbs in 1902.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.

The third law of thermodynamics states, regarding the properties of closed systems in thermodynamic equilibrium:
The entropy of a system approaches a constant value when its temperature approaches absolute zero.
In statistical mechanics, a semi-classical derivation of entropy that does not take into account the indistinguishability of particles yields an expression for entropy which is not extensive. This leads to a paradox known as the Gibbs paradox, after Josiah Willard Gibbs, who proposed this thought experiment in 1874‒1875. The paradox allows for the entropy of closed systems to decrease, violating the second law of thermodynamics. A related paradox is the "mixing paradox". If one takes the perspective that the definition of entropy must be changed so as to ignore particle permutation, the paradox is averted.
In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless.
In classical statistical mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency to decrease in the quantity H in a nearly-ideal gas of molecules. As this quantity H was meant to represent the entropy of thermodynamics, the H-theorem was an early demonstration of the power of statistical mechanics as it claimed to derive the second law of thermodynamics—a statement about fundamentally irreversible processes—from reversible microscopic mechanics. It is thought to prove the second law of thermodynamics, albeit under the assumption of low-entropy initial conditions.

Ludwig Eduard Boltzmann was an Austrian physicist and philosopher. His greatest achievements were the development of statistical mechanics, and the statistical explanation of the second law of thermodynamics. In 1877 he provided the current definition of entropy, , where Ω is the number of microstates whose energy equals the system's energy, interpreted as a measure of statistical disorder of a system. Max Planck named the constant kB the Boltzmann constant.
In statistical mechanics, the grand canonical ensemble is the statistical ensemble that is used to represent the possible states of a mechanical system of particles that are in thermodynamic equilibrium with a reservoir. The system is said to be open in the sense that the system can exchange energy and particles with a reservoir, so that various possible states of the system can differ in both their total energy and total number of particles. The system's volume, shape, and other external coordinates are kept the same in all possible states of the system.

In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations. In contrast, the macrostate of a system refers to its macroscopic properties, such as its temperature, pressure, volume and density. Treatments on statistical mechanics define a macrostate as follows: a particular set of values of energy, the number of particles, and the volume of an isolated thermodynamic system is said to specify a particular macrostate of it. In this description, microstates appear as different possible ways the system can achieve a particular macrostate.
The mathematical expressions for thermodynamic entropy in the statistical thermodynamics formulation established by Ludwig Boltzmann and J. Willard Gibbs in the 1870s are similar to the information entropy by Claude Shannon and Ralph Hartley, developed in the 1940s.
The concept entropy was first developed by German physicist Rudolf Clausius in the mid-nineteenth century as a thermodynamic property that predicts that certain spontaneous processes are irreversible or impossible. In statistical mechanics, entropy is formulated as a statistical property using probability theory. The statistical entropy perspective was introduced in 1870 by Austrian physicist Ludwig Boltzmann, who established a new field of physics that provided the descriptive linkage between the macroscopic observation of nature and the microscopic view based on the rigorous treatment of a large ensembles of microstates that constitute thermodynamic systems.
Conformational entropy is the entropy associated with the number of conformations of a molecule. The concept is most commonly applied to biological macromolecules such as proteins and RNA, but also be used for polysaccharides and other molecules. To calculate the conformational entropy, the possible conformations of the molecule may first be discretized into a finite number of states, usually characterized by unique combinations of certain structural parameters, each of which has been assigned an energy. In proteins, backbone dihedral angles and side chain rotamers are commonly used as parameters, and in RNA the base pairing pattern may be used. These characteristics are used to define the degrees of freedom. The conformational entropy associated with a particular structure or state, such as an alpha-helix, a folded or an unfolded protein structure, is then dependent on the probability of the occupancy of that structure.

In thermodynamics, entropy is a numerical quantity that shows that many physical processes can go in only one direction in time. For example, you can pour cream into coffee and mix it, but you cannot "unmix" it; you can burn a piece of wood, but you cannot "unburn" it. The word 'entropy' has entered popular usage to refer a lack of order or predictability, or of a gradual decline into disorder. A more physical interpretation of thermodynamic entropy refers to spread of energy or matter, or to extent and diversity of microscopic motion.

This article is a summary of common equations and quantities in thermodynamics.
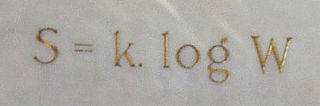
In statistical mechanics, Boltzmann's equation is a probability equation relating the entropy , also written as , of an ideal gas to the multiplicity, the number of real microstates corresponding to the gas's macrostate:
The partition function or configuration integral, as used in probability theory, information theory and dynamical systems, is a generalization of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann distribution. The partition function occurs in many problems of probability theory because, in situations where there is a natural symmetry, its associated probability measure, the Gibbs measure, has the Markov property. This means that the partition function occurs not only in physical systems with translation symmetry, but also in such varied settings as neural networks, and applications such as genomics, corpus linguistics and artificial intelligence, which employ Markov networks, and Markov logic networks. The Gibbs measure is also the unique measure that has the property of maximizing the entropy for a fixed expectation value of the energy; this underlies the appearance of the partition function in maximum entropy methods and the algorithms derived therefrom.