In geometry, confocal means having the same foci: confocal conic sections.
 | This article includes a list of related items that share the same name (or similar names). If an internal link incorrectly led you here, you may wish to change the link to point directly to the intended article. |
In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
In mathematics, the matrix representation of conic sections permits the tools of linear algebra to be used in the study of conic sections. It provides easy ways to calculate a conic section's axis, vertices, tangents and the pole and polar relationship between points and lines of the plane determined by the conic. The technique does not require putting the equation of a conic section into a standard form, thus making it easier to investigate those conic sections whose axes are not parallel to the coordinate system.
In geometry, a degenerate conic is a conic that fails to be an irreducible curve. This means that the defining equation is factorable over the complex numbers as the product of two linear polynomials.
In geometry, the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and the plane is a conic section, and the point at which either sphere touches the plane is a focus of the conic section, so the Dandelin spheres are also sometimes called focal spheres.
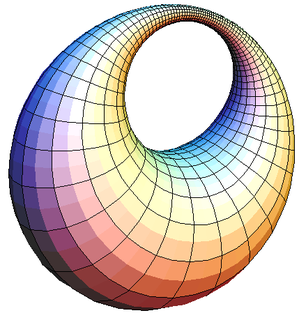
In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter are themselves examples of Dupin cyclides. They were discovered by Charles Dupin in his 1803 dissertation under Gaspard Monge. The key property of a Dupin cyclide is that it is a channel surface in two different ways. This property means that Dupin cyclides are natural objects in Lie sphere geometry.
In astrodynamics an orbit equation defines the path of orbiting body around central body relative to , without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance, has an orbit that is a conic section with the central body located at one of the two foci, or the focus.
In geometry, focuses or foci, singular focus, are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse.
Confocal microscopy, most frequently confocal laser scanning microscopy (CLSM) or laser confocal scanning microscopy (LCSM), is an optical imaging technique for increasing optical resolution and contrast of a micrograph by means of using a spatial pinhole to block out-of-focus light in image formation. Capturing multiple two-dimensional images at different depths in a sample enables the reconstruction of three-dimensional structures within an object. This technique is used extensively in the scientific and industrial communities and typical applications are in life sciences, semiconductor inspection and materials science.
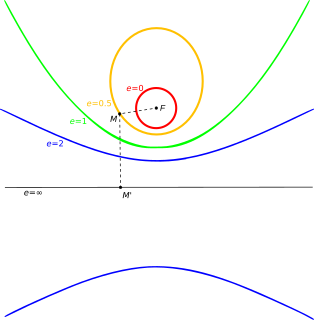
In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape.
Menaechmus was an ancient Greek mathematician, geometer and philosopher born in Alopeconnesus or Prokonnesos in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube using the parabola and hyperbola.
A Cassini oval is a quartic plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This may be contrasted with an ellipse, for which the sum of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree 2.
Perseus was an ancient Greek geometer, who invented the concept of spiric sections, in analogy to the conic sections studied by Apollonius of Perga.
In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the widest points of the perimeter.
In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter. For example, two diameters of a circle are conjugate if and only if they are perpendicular.
In geometry, the director circle of an ellipse or hyperbola is a circle consisting of all points where two perpendicular tangent lines to the ellipse or hyperbola cross each other.
In mathematics, a generalized conic is a geometrical object defined by a property which is a generalization of some defining property of the classical conic. For example, in elementary geometry, an ellipse can be defined as the locus of a point which moves in a plane such that the sum of its distances from two fixed points – the foci – in the plane is a constant. The curve obtained when the set of two fixed points is replaced by an arbitrary, but fixed, finite set of points in the plane is called an n–ellipse and can be thought of as a generalized ellipse. Since an ellipse is the equidistant set of two circles, the equidistant set of two arbitrary sets of points in a plane can be viewed as a generalized conic. In rectangular Cartesian coordinates, the equation y = x2 represents a parabola. The generalized equation y = xr, for r ≠ 0 and r ≠ 1, can be treated as defining a generalized parabola. The idea of generalized conic has found applications in approximation theory and optimization theory.
In geometry, two conic sections are called confocal, if they have the same foci. Because ellipses and hyperbolas possess two foci, there are confocal ellipses, confocal hyperbolas and confocal mixtures of ellipses and hyperbolas. In the mixture of confocal ellipses and hyperbolas, any ellipse intersects any hyperbola orthogonally. Parabolas possess only one focus, so, by convention, confocal parabolas have the same focus and the same axis of symmetry. Consequently, any point not on the axis of symmetry lies on two confocal parabolas which intersect orthogonally.
In geometry, focal conics are a pair of curves consisting of either