In universal algebra, a congruence-permutable algebra is an algebra whose congruences commute under composition. This symmetry has several equivalent characterizations, which lend to the analysis of such algebras. Many familiar varieties of algebras, such as the variety of groups, consist of congruence-permutable algebras, but some, like the variety of lattices, have members that are not congruence-permutable.
Given an algebra , a pair of congruences are said to permute when . [1] :121 An algebra is called congruence-permutable when each pair of congruences of permute. [1] :122 A variety of algebras is referred to as congruence-permutable when every algebra in is congruence-permutable. [1] :122
In 1954 Maltsev gave two other conditions that are equivalent to the one given above defining a congruence-permutable variety of algebras. This initiated the study of congruence-permutable varieties. [1] :122
Suppose that is a variety of algebras. The following are equivalent:
Such a term is called a Maltsev term and congruence-permutable varieties are also known as Maltsev varieties in his honor. [1] :122
Most classical varieties in abstract algebra, such as groups [1] :123, rings [1] :123, and Lie algebras [ citation needed ] are congruence-permutable. Any variety that contains a group operation is congruence-permutable, and the Maltsev term is .[ citation needed ]
Viewed as a lattice the chain with three elements is not congruence-permutable and hence neither is the variety of lattices. [1] :123
In mathematics, any vector space V has a corresponding dual vector space consisting of all linear functionals on V, together with the vector space structure of pointwise addition and scalar multiplication by constants.
In algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by , is the set of all prime ideals of R. It is commonly augmented with the Zariski topology and with a structure sheaf, turning it into a locally ringed space. A locally ringed space of this form is called an affine scheme.
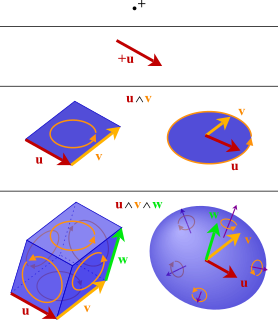
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors u and v, denoted by u ∧ v, is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of u ∧ v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. Like the cross product, the exterior product is anticommutative, meaning that u ∧ v = −(v ∧ u) for all vectors u and v, but, unlike the cross product, the exterior product is associative. One way to visualize a bivector is as a family of parallelograms all lying in the same plane, having the same area, and with the same orientation—a choice of clockwise or counterclockwise.
In mathematics, the adele ring of a global field is a central object of class field theory, a branch of algebraic number theory. It is the restricted product of all the completions of the global field, and is an example of a self-dual topological ring.
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry. In most of these theories, the even elements of the superalgebra correspond to bosons and odd elements to fermions.
In mathematics, a quotient algebra is the result of partitioning the elements of an algebraic structure using a congruence relation. Quotient algebras are also called factor algebras. Here, the congruence relation must be an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense described below. Its equivalence classes partition the elements of the given algebraic structure. The quotient algebra has these classes as its elements, and the compatibility conditions are used to give the classes an algebraic structure.
In mathematics and theoretical physics, the term quantum group denotes one of a few different kinds of noncommutative algebras with additional structure. These include Drinfeld–Jimbo type quantum groups, compact matrix quantum groups, and bicrossproduct quantum groups.
In algebraic geometry, motives is a theory proposed by Alexander Grothendieck in the 1960s to unify the vast array of similarly behaved cohomology theories such as singular cohomology, de Rham cohomology, etale cohomology, and crystalline cohomology. Philosophically, a 'motif' is the 'cohomology essence' of a variety.
In Bayesian probability theory, if the posterior distributions p(θ | x) are in the same probability distribution family as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood function p(x | θ). For example, the Gaussian family is conjugate to itself with respect to a Gaussian likelihood function: if the likelihood function is Gaussian, choosing a Gaussian prior over the mean will ensure that the posterior distribution is also Gaussian. This means that the Gaussian distribution is a conjugate prior for the likelihood that is also Gaussian. The concept, as well as the term "conjugate prior", were introduced by Howard Raiffa and Robert Schlaifer in their work on Bayesian decision theory. A similar concept had been discovered independently by George Alfred Barnard.
In commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its p-th power. In certain contexts it is an automorphism, but this is not true in general.
In linear algebra, a basis for a vector space is a linearly independent set spanning the vector space. This article deals mainly with finite-dimensional vector spaces, but many of the theorems are also valid for infinite-dimensional vector spaces. A basis for a vector space of dimension n is a set of n vectors (α1, …, αn), called basis vectors, with the property that every vector in the space can be expressed as a unique linear combination of the basis vectors. The matrix representations of operators are also determined by the chosen basis. Since it is often desirable to work with more than one basis for a vector space, it is of fundamental importance in linear algebra to be able to easily transform coordinate-wise representations of vectors and operators taken with respect to one basis to their equivalent representations with respect to another basis. Such a transformation is called a change of basis. For example, if is a matrix whose columns comprise a basis of , a vector can also be expressed as a linear combination of 's columns by the vector . By definition then, . If 's columns form an orthonormal basis, then 's inverse is its transpose and we have the change of basis as , i.e. the vector of 's scalar projections onto the columns of .
In mathematics, specifically in category theory, an -coalgebra is a structure defined according to a functor , with specific properties as defined below. For both algebra and coalgebra, a functor is a convenient and general way of organizing a signature. This has applications in computer science: examples of coalgebras include lazy, infinite data structures, such as streams, and also transition systems.
In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since each chart lies within a linear space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.
The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.
In mathematics, the congruence lattice problem asks whether every algebraic distributive lattice is isomorphic to the congruence lattice of some other lattice. The problem was posed by Robert P. Dilworth, and for many years it was one of the most famous and long-standing open problems in lattice theory; it had a deep impact on the development of lattice theory itself. The conjecture that every distributive lattice is a congruence lattice is true for all distributive lattices with at most ℵ1 compact elements, but F. Wehrung provided a counterexample for distributive lattices with ℵ2 compact elements using a construction based on Kuratowski's free set theorem.
In the mathematical field of abstract algebra, isotopy is an equivalence relation used to classify the algebraic notion of loop.
In mathematics, the structure constants or structure coefficients of an algebra over a field are used to explicitly specify the product of two basis vectors in the algebra as a linear combination. Given the structure constants, the resulting product is bilinear and can be uniquely extended to all vectors in the vector space, thus uniquely determining the product for the algebra.
In mathematics, the Kodaira–Spencer map, introduced by Kunihiko Kodaira and Donald C. Spencer, is a map associated to a deformation of a scheme or complex manifold X, taking a tangent space of a point of the deformation space to the first cohomology group of the sheaf of vector fields on X.
In mathematics, the exterior algebra has a rich algebraic structure. The exterior algebra of vector fields on manifolds has an even richer structure driven by the interplay of differentiation on the manifold with the properties of the exterior algebra. This article summarizes several identities in exterior calculus.
Tau functions are an important ingredient in the modern theory of integrable systems, and have numerous applications in a variety of other domains. Before being named as such, they were effectively introduced by Ryogo Hirota in his direct method approach to integrable systems, based on expressing them in an equivalent bilinear form. The term Tau function, or -function, was first used systematically by Mikio Sato and his students in the specific context of the Kadomtsev–Petviashvili equation, and related integrable hierarchies. It is a central ingredient in the theory of solitons. Tau functions also appear as matrix model partition functions in the spectral theory of Random Matrices, and may also serve as generating functions, in the sense of combinatorics and enumerative geometry, especially in relation to moduli spaces of Riemann surfaces, and enumeration of branched coverings, or so-called Hurwitz numbers.
 | This abstract algebra-related article is a stub. You can help Wikipedia by expanding it. |
