 | This article includes a list of general references, but it lacks sufficient corresponding inline citations .(October 2011) |
Conic optimization is a subfield of convex optimization that studies problems consisting of minimizing a convex function over the intersection of an affine subspace and a convex cone.
The class of conic optimization problems includes some of the most well known classes of convex optimization problems, namely linear and semidefinite programming.
Given a real vector space X, a convex, real-valued function
defined on a convex cone , and an affine subspace defined by a set of affine constraints , a conic optimization problem is to find the point in for which the number is smallest.
Examples of include the positive orthant , positive semidefinite matrices , and the second-order cone. Often is a linear function, in which case the conic optimization problem reduces to a linear program, a semidefinite program, and a second order cone program, respectively.
Certain special cases of conic optimization problems have notable closed-form expressions of their dual problems.
The dual of the conic linear program
is
where denotes the dual cone of .
Whilst weak duality holds in conic linear programming, strong duality does not necessarily hold. [1]
The dual of a semidefinite program in inequality form
is given by
The Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed vector space to make the study of the dual space "interesting". Another version of the Hahn–Banach theorem is known as the Hahn–Banach separation theorem or the hyperplane separation theorem, and has numerous uses in convex geometry.
In mathematics, a linear form is a linear map from a vector space to its field of scalars.
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. Such involutions sometimes have fixed points, so that the dual of A is A itself. For example, Desargues' theorem is self-dual in this sense under the standard duality in projective geometry.
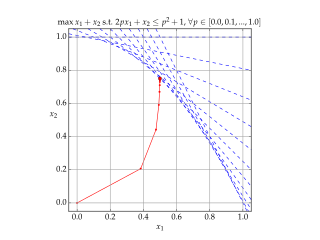
Interior-point methods are algorithms for solving linear and non-linear convex optimization problems. IPMs combine two advantages of previously-known algorithms:
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets. Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard.
In mathematical optimization, the Karush–Kuhn–Tucker (KKT) conditions, also known as the Kuhn–Tucker conditions, are first derivative tests for a solution in nonlinear programming to be optimal, provided that some regularity conditions are satisfied.
In mathematics, Farkas' lemma is a solvability theorem for a finite system of linear inequalities. It was originally proven by the Hungarian mathematician Gyula Farkas. Farkas' lemma is the key result underpinning the linear programming duality and has played a central role in the development of mathematical optimization. It is used amongst other things in the proof of the Karush–Kuhn–Tucker theorem in nonlinear programming. Remarkably, in the area of the foundations of quantum theory, the lemma also underlies the complete set of Bell inequalities in the form of necessary and sufficient conditions for the existence of a local hidden-variable theory, given data from any specific set of measurements.
In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. If the primal is a minimization problem then the dual is a maximization problem. Any feasible solution to the primal (minimization) problem is at least as large as any feasible solution to the dual (maximization) problem. Therefore, the solution to the primal is an upper bound to the solution of the dual, and the solution of the dual is a lower bound to the solution of the primal. This fact is called weak duality.
In linear algebra, a cone—sometimes called a linear cone for distinguishing it from other sorts of cones—is a subset of a vector space that is closed under positive scalar multiplication; that is, C is a cone if implies for every positive scalar s.
In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions. The ellipsoid method generates a sequence of ellipsoids whose volume uniformly decreases at every step, thus enclosing a minimizer of a convex function.
Semidefinite programming (SDP) is a subfield of convex optimization concerned with the optimization of a linear objective function over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron.
In convex optimization, a linear matrix inequality (LMI) is an expression of the form
A second-order cone program (SOCP) is a convex optimization problem of the form
In mathematics, an ordered vector space or partially ordered vector space is a vector space equipped with a partial order that is compatible with the vector space operations.
A geometric program (GP) is an optimization problem of the form
A self-concordant function is a function satisfying a certain differential inequality, which makes it particularly easy for optimization using Newton's method A self-concordant barrier is a particular self-concordant function, that is also a barrier function for a particular convex set. Self-concordant barriers are important ingredients in interior point methods for optimization.
In convex geometry, a spectrahedron is a shape that can be represented as a linear matrix inequality. Alternatively, the set of n × n positive semidefinite matrices forms a convex cone in Rn × n, and a spectrahedron is a shape that can be formed by intersecting this cone with an affine subspace.
A sum-of-squares optimization program is an optimization problem with a linear cost function and a particular type of constraint on the decision variables. These constraints are of the form that when the decision variables are used as coefficients in certain polynomials, those polynomials should have the polynomial SOS property. When fixing the maximum degree of the polynomials involved, sum-of-squares optimization is also known as the Lasserre hierarchy of relaxations in semidefinite programming.
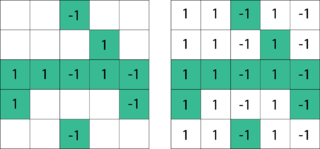
Matrix completion is the task of filling in the missing entries of a partially observed matrix, which is equivalent to performing data imputation in statistics. A wide range of datasets are naturally organized in matrix form. One example is the movie-ratings matrix, as appears in the Netflix problem: Given a ratings matrix in which each entry represents the rating of movie by customer , if customer has watched movie and is otherwise missing, we would like to predict the remaining entries in order to make good recommendations to customers on what to watch next. Another example is the document-term matrix: The frequencies of words used in a collection of documents can be represented as a matrix, where each entry corresponds to the number of times the associated term appears in the indicated document.
Quantum optimization algorithms are quantum algorithms that are used to solve optimization problems. Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. Quantum computing may allow problems which are not practically feasible on classical computers to be solved, or suggest a considerable speed up with respect to the best known classical algorithm.
