
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals.

In mathematics, convolution is a mathematical operation on two functions that produces a third function. The term convolution refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result. Graphically, it expresses how the 'shape' of one function is modified by the other.
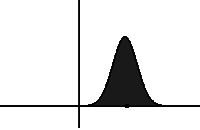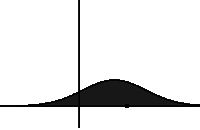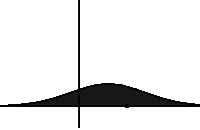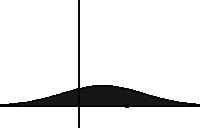
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker-Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc.

In applied mathematics, discretization is the process of transferring continuous functions, models, variables, and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers. Dichotomization is the special case of discretization in which the number of discrete classes is 2, which can approximate a continuous variable as a binary variable.

In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy.
The adiabatic theorem is a concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock (1928), was stated as follows:
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.
In pulsed radar and sonar signal processing, an ambiguity function is a two-dimensional function of propagation delay and Doppler frequency , . It represents the distortion of a returned pulse due to the receiver matched filter of the return from a moving target. The ambiguity function is defined by the properties of the pulse and of the filter, and not any particular target scenario.
In probability theory and statistics, given a stochastic process, the autocovariance is a function that gives the covariance of the process with itself at pairs of time points. Autocovariance is closely related to the autocorrelation of the process in question.
In scattering theory, a part of mathematical physics, the Dyson series, formulated by Freeman Dyson, is a perturbative expansion of the time evolution operator in the interaction picture. Each term can be represented by a sum of Feynman diagrams.
A cyclostationary process is a signal having statistical properties that vary cyclically with time. A cyclostationary process can be viewed as multiple interleaved stationary processes. For example, the maximum daily temperature in New York City can be modeled as a cyclostationary process: the maximum temperature on July 21 is statistically different from the temperature on December 20; however, it is a reasonable approximation that the temperature on December 20 of different years has identical statistics. Thus, we can view the random process composed of daily maximum temperatures as 365 interleaved stationary processes, each of which takes on a new value once per year.
In mathematics, delay differential equations (DDEs) are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times. DDEs are also called time-delay systems, systems with aftereffect or dead-time, hereditary systems, equations with deviating argument, or differential-difference equations. They belong to the class of systems with the functional state, i.e. partial differential equations (PDEs) which are infinite dimensional, as opposed to ordinary differential equations (ODEs) having a finite dimensional state vector. Four points may give a possible explanation of the popularity of DDEs:
- Aftereffect is an applied problem: it is well known that, together with the increasing expectations of dynamic performances, engineers need their models to behave more like the real process. Many processes include aftereffect phenomena in their inner dynamics. In addition, actuators, sensors, and communication networks that are now involved in feedback control loops introduce such delays. Finally, besides actual delays, time lags are frequently used to simplify very high order models. Then, the interest for DDEs keeps on growing in all scientific areas and, especially, in control engineering.
- Delay systems are still resistant to many classical controllers: one could think that the simplest approach would consist in replacing them by some finite-dimensional approximations. Unfortunately, ignoring effects which are adequately represented by DDEs is not a general alternative: in the best situation, it leads to the same degree of complexity in the control design. In worst cases, it is potentially disastrous in terms of stability and oscillations.
- Voluntary introduction of delays can benefit the control system.
- In spite of their complexity, DDEs often appear as simple infinite-dimensional models in the very complex area of partial differential equations (PDEs).

The Wigner distribution function (WDF) is used in signal processing as a transform in time-frequency analysis.
In control theory, the minimum energy control is the control that will bring a linear time invariant system to a desired state with a minimum expenditure of energy.
In control theory, we may need to find out whether or not a system such as
A Modified Wigner distribution function is a variation of the Wigner distribution function (WD) with reduced or removed cross-terms.
In mathematics, the reduced derivative is a generalization of the notion of derivative that is well-suited to the study of functions of bounded variation. Although functions of bounded variation have derivatives in the sense of Radon measures, it is desirable to have a derivative that takes values in the same space as the functions themselves. Although the precise definition of the reduced derivative is quite involved, its key properties are quite easy to remember:
In control theory, the state-transition matrix is a matrix whose product with the state vector at an initial time gives at a later time . The state-transition matrix can be used to obtain the general solution of linear dynamical systems.

In applied probability, a regenerative process is a class of stochastic process with the property that certain portions of the process can be treated as being statistically independent of each other. This property can be used in the derivation of theoretical properties of such processes.
In stochastic processes, Kramers–Moyal expansion refers to a Taylor series expansion of the master equation, named after Hans Kramers and José Enrique Moyal. In many textbooks, the expansion is used only to derive the Fokker–Planck equation, and never used again. In general, continuous stochastic processes are essentially all Markovian, and so Fokker–Planck equations are sufficient for studying them. The higher-order Kramers–Moyal expansion only come into play when the process is jumpy. This usually means it is a Poisson-like process.





























































