
The Shapley value is a solution concept in cooperative game theory. It was named in honor of Lloyd Shapley, who introduced it in 1951 and won the Nobel Memorial Prize in Economic Sciences for it in 2012. To each cooperative game it assigns a unique distribution of a total surplus generated by the coalition of all players. The Shapley value is characterized by a collection of desirable properties. Hart (1989) provides a survey of the subject.
In game theory, a cooperative game is a game with competition between groups of players ("coalitions") due to the possibility of external enforcement of cooperative behavior. Those are opposed to non-cooperative games in which there is either no possibility to forge alliances or all agreements need to be self-enforcing.
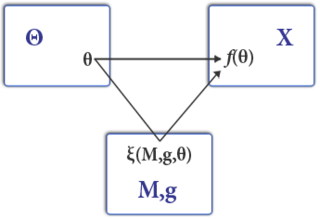
Mechanism design is a field in economics and game theory that takes an objectives-first approach to designing economic mechanisms or incentives, toward desired objectives, in strategic settings, where players act rationally. Because it starts at the end of the game, then goes backwards, it is also called reverse game theory. It has broad applications, from economics and politics in fields such as market design, auction theory and social choice theory to networked-systems.
In game theory, an asymmetric game where players have private information is said to be strategy-proof or strategyproof (SP) if it is a weakly-dominant strategy for every player to reveal his/her private information, i.e. given no information about what the others do, you fare best or at least not worse by being truthful.

A Vickrey auction or sealed-bid second-price auction (SBSPA) is a type of sealed-bid auction. Bidders submit written bids without knowing the bid of the other people in the auction. The highest bidder wins but the price paid is the second-highest bid. This type of auction is strategically similar to an English auction and gives bidders an incentive to bid their true value. The auction was first described academically by Columbia University professor William Vickrey in 1961 though it had been used by stamp collectors since 1893. In 1797 Johann Wolfgang von Goethe sold a manuscript using a sealed-bid, second-price auction.
In cooperative game theory, the core is the set of feasible allocations or imputations where no coalition of agents can benefit by breaking away from the grand coalition. One can think of the core corresponding to situations where it is possible to sustain cooperation among all agents. A coalition is said to improve upon or block a feasible allocation if the members of that coalition can generate more value among themselves than they are allocated in the original allocation. As such, that coalition is not incentivized to stay with the grand coalition.
A Lindahl tax is a form of taxation conceived by Erik Lindahl in which individuals pay for public goods according to their marginal benefits. In other words, they pay according to the amount of satisfaction or utility they derive from the consumption of an additional unit of the public good. Lindahl taxation is designed to maximize efficiency for each individual and provide the optimal level of a public good.

A double auction is a process of buying and selling goods with multiple sellers and multiple buyers. Potential buyers submit their bids and potential sellers submit their ask prices to the market institution, and then the market institution chooses some price p that clears the market: all the sellers who asked less than p sell and all buyers who bid more than p buy at this price p. Buyers and sellers that bid or ask for exactly p are also included. A common example of a double auction is stock exchange.
Competitive equilibrium is a concept of economic equilibrium, introduced by Kenneth Arrow and Gérard Debreu in 1951, appropriate for the analysis of commodity markets with flexible prices and many traders, and serving as the benchmark of efficiency in economic analysis. It relies crucially on the assumption of a competitive environment where each trader decides upon a quantity that is so small compared to the total quantity traded in the market that their individual transactions have no influence on the prices. Competitive markets are an ideal standard by which other market structures are evaluated.

A Vickrey–Clarke–Groves (VCG) auction is a type of sealed-bid auction of multiple items. Bidders submit bids that report their valuations for the items, without knowing the bids of the other bidders. The auction system assigns the items in a socially optimal manner: it charges each individual the harm they cause to other bidders. It gives bidders an incentive to bid their true valuations, by ensuring that the optimal strategy for each bidder is to bid their true valuations of the items; it can be undermined by bidder collusion and in particular in some circumstances by a single bidder making multiple bids under different names. It is a generalization of a Vickrey auction for multiple items.

Market design is a practical methodology for creation of markets of certain properties, which is partially based on mechanism design. In some markets, prices may be used to induce the desired outcomes — these markets are the study of auction theory. In other markets, prices may not be used — these markets are the study of matching theory.

The Shapley–Folkman lemma is a result in convex geometry that describes the Minkowski addition of sets in a vector space. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the economist Ross M. Starr.
In mechanism design, a Vickrey–Clarke–Groves (VCG) mechanism is a generic truthful mechanism for achieving a socially-optimal solution. It is a generalization of a Vickrey–Clarke–Groves auction. A VCG auction performs a specific task: dividing items among people. A VCG mechanism is more general: it can be used to select any outcome out of a set of possible outcomes.
In mechanism design, an agent is said to have single-parameter utility if his valuation of the possible outcomes can be represented by a single number. For example, in an auction for a single item, the utilities of all agents are single-parametric, since they can be represented by their monetary evaluation of the item. In contrast, in a combinatorial auction for two or more related items, the utilities are usually not single-parametric, since they are usually represented by their evaluations to all possible bundles of items.
A Bayesian-optimal mechanism (BOM) is a mechanism in which the designer does not know the valuations of the agents for whom the mechanism is designed, but the designer knows that they are random variables and knows the probability distribution of these variables.
Rental harmony is a kind of a fair division problem in which indivisible items and a fixed monetary cost have to be divided simultaneously. The housemates problem and room-assignment-rent-division are alternative names to the same problem.
A sequential auction is an auction in which several items are sold, one after the other, to the same group of potential buyers. In a sequential first-price auction (SAFP), each individual item is sold using a first price auction, while in a sequential second-price auction (SASP), each individual item is sold using a second price auction.

The Price of Anarchy (PoA) is a concept in game theory and mechanism design that measures how the social welfare of a system degrades due to selfish behavior of its agents. It has been studied extensively in various contexts, particularly in auctions.
Fair allocation of items and money is a class of fair item allocation problems in which, during the allocation process, it is possible to give or take money from some of the participants. Without money, it may be impossible to allocate indivisible items fairly. For example, if there is one item and two people, and the item must be given entirely to one of them, the allocation will be unfair towards the other one. Monetary payments make it possible to attain fairness, as explained below.
The welfare maximization problem is an optimization problem studied in economics and computer science. Its goal is to partition a set of items among agents with different utility functions, such that the welfare – defined as the sum of the agents' utilities – is as high as possible. In other words, the goal is to find an item allocation satisfying the utilitarian rule.















