
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.
In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses.

In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple and star polygons.
In Euclidean geometry, a regular polygon is a polygon that is direct equiangular and equilateral. Regular polygons may be either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.

In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.

In geometry, a curve of constant width is a simple closed curve in the plane whose width is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.

In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.

Tom Mike Apostol was an American analytic number theorist and professor at the California Institute of Technology, best known as the author of widely used mathematical textbooks.

In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson. The concept was first published, however, by William Wallace in 1799.

In plane geometry, Holditch's theorem states that if a chord of fixed length is allowed to rotate inside a convex closed curve, then the locus of a point on the chord a distance p from one end and a distance q from the other is a closed curve whose enclosed area is less than that of the original curve by . The theorem was published in 1858 by Rev. Hamnet Holditch. While not mentioned by Holditch, the proof of the theorem requires an assumption that the chord be short enough that the traced locus is a simple closed curve.

The four-vertex theorem of geometry states that the curvature along a simple, closed, smooth plane curve has at least four local extrema. The name of the theorem derives from the convention of calling an extreme point of the curvature function a vertex. This theorem has many generalizations, including a version for space curves where a vertex is defined as a point of vanishing torsion.
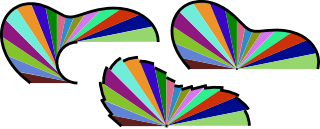
Visual calculus, invented by Mamikon Mnatsakanian, is an approach to solving a variety of integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculation, often reminiscent of what Martin Gardner called "aha! solutions" or Roger Nelsen a proof without words.

In geometry, two or more objects are said to be concentric when they share the same center. Any pair of objects with well-defined centers can be concentric, including circles, spheres, regular polygons, regular polyhedra, parallelograms, cones, conic sections, and quadrics.

In Euclidean geometry, a tangential polygon, also known as a circumscribed polygon, is a convex polygon that contains an inscribed circle. This is a circle that is tangent to each of the polygon's sides. The dual polygon of a tangential polygon is a cyclic polygon, which has a circumscribed circle passing through each of its vertices.
In mathematics, a generalized conic is a geometrical object defined by a property which is a generalization of some defining property of the classical conic. For example, in elementary geometry, an ellipse can be defined as the locus of a point which moves in a plane such that the sum of its distances from two fixed points – the foci – in the plane is a constant. The curve obtained when the set of two fixed points is replaced by an arbitrary, but fixed, finite set of points in the plane is called an n–ellipse and can be thought of as a generalized ellipse. Since an ellipse is the equidistant set of two circles, the equidistant set of two arbitrary sets of points in a plane can be viewed as a generalized conic. In rectangular Cartesian coordinates, the equation y = x2 represents a parabola. The generalized equation y = xr, for r ≠ 0 and r ≠ 1, can be treated as defining a generalized parabola. The idea of generalized conic has found applications in approximation theory and optimization theory.

In mathematics and particularly in elementary geometry, a circumgon is a geometric figure which circumscribes some circle, in the sense that it is the union of the outer edges of non-overlapping triangles each of which has a vertex at the center of the circle and opposite side on a line that is tangent to the circle. The limiting case in which part or all of the circumgon is a circular arc is permitted. A circumgonal region is the union of those triangular regions.
























