The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In fluid mechanics, hydrostatic equilibrium is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the planetary atmosphere into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space. In general, it is what causes objects in space to be spherical.

An aerosol is a suspension of fine solid particles or liquid droplets in air or another gas. Aerosols can be generated from natural or human causes. The term aerosol commonly refers to the mixture of particulates in air, and not to the particulate matter alone. Examples of natural aerosols are fog, mist or dust. Examples of human caused aerosols include particulate air pollutants, mist from the discharge at hydroelectric dams, irrigation mist, perfume from atomizers, smoke, dust, sprayed pesticides, and medical treatments for respiratory illnesses.

Bernoulli's principle is a key concept in fluid dynamics that relates pressure, density, speed and height. Bernoulli's principle states that an increase in the speed of a parcel of fluid occurs simultaneously with a decrease in either the pressure or the height above a datum. The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book Hydrodynamica in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form.
The vorticity equation of fluid dynamics describes the evolution of the vorticity ω of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:
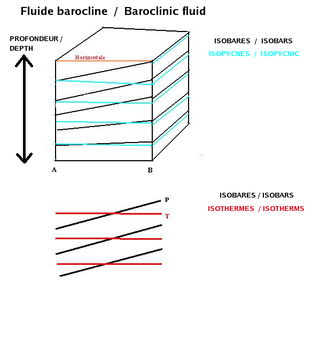
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure. A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.

Terminal velocity is the maximum speed attainable by an object as it falls through a fluid. It is reached when the sum of the drag force (Fd) and the buoyancy is equal to the downward force of gravity (FG) acting on the object. Since the net force on the object is zero, the object has zero acceleration. For objects falling through air at normal pressure, the buoyant force is usually dismissed and not taken into account, as its effects are negligible.

Settling is the process by which particulates move towards the bottom of a liquid and form a sediment. Particles that experience a force, either due to gravity or due to centrifugal motion will tend to move in a uniform manner in the direction exerted by that force. For gravity settling, this means that the particles will tend to fall to the bottom of the vessel, forming sludge or slurry at the vessel base. Settling is an important operation in many applications, such as mining, wastewater and drinking water treatment, biological science, space propellant reignition, and scooping.
In viscous fluid dynamics, the Archimedes number (Ar), is a dimensionless number used to determine the motion of fluids due to density differences, named after the ancient Greek scientist and mathematician Archimedes.
Quantum turbulence is the name given to the turbulent flow – the chaotic motion of a fluid at high flow rates – of quantum fluids, such as superfluids. The idea that a form of turbulence might be possible in a superfluid via the quantized vortex lines was first suggested by Richard Feynman. The dynamics of quantum fluids are governed by quantum mechanics, rather than classical physics which govern classical (ordinary) fluids. Some examples of quantum fluids include superfluid helium, Bose–Einstein condensates (BECs), polariton condensates, and nuclear pasta theorized to exist inside neutron stars. Quantum fluids exist at temperatures below the critical temperature at which Bose-Einstein condensation takes place.
In fluid dynamics, drag, sometimes referred to as fluid resistance, is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers, two solid surfaces, or between a fluid and a solid surface. Drag forces tend to decrease fluid velocity relative to the solid object in the fluid's path.

A fluidized bed is a physical phenomenon that occurs when a solid particulate substance is under the right conditions so that it behaves like a fluid. The usual way to achieve a fluidized bed is to pump pressurized fluid into the particles. The resulting medium then has many properties and characteristics of normal fluids, such as the ability to free-flow under gravity, or to be pumped using fluid technologies.

A dust collector is a system used to enhance the quality of air released from industrial and commercial processes by collecting dust and other impurities from air or gas. Designed to handle high-volume dust loads, a dust collector system consists of a blower, dust filter, a filter-cleaning system, and a dust receptacle or dust removal system. It is distinguished from air purifiers, which use disposable filters to remove dust.

In fluid dynamics, an eddy is the swirling of a fluid and the reverse current created when the fluid is in a turbulent flow regime. The moving fluid creates a space devoid of downstream-flowing fluid on the downstream side of the object. Fluid behind the obstacle flows into the void creating a swirl of fluid on each edge of the obstacle, followed by a short reverse flow of fluid behind the obstacle flowing upstream, toward the back of the obstacle. This phenomenon is naturally observed behind large emergent rocks in swift-flowing rivers.

The lattice Boltzmann methods (LBM), originated from the lattice gas automata (LGA) method (Hardy-Pomeau-Pazzis and Frisch-Hasslacher-Pomeau models), is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solving the Navier–Stokes equations directly, a fluid density on a lattice is simulated with streaming and collision (relaxation) processes. The method is versatile as the model fluid can straightforwardly be made to mimic common fluid behaviour like vapour/liquid coexistence, and so fluid systems such as liquid droplets can be simulated. Also, fluids in complex environments such as porous media can be straightforwardly simulated, whereas with complex boundaries other CFD methods can be hard to work with.
The Kutta–Joukowski theorem is a fundamental theorem in aerodynamics used for the calculation of lift of an airfoil translating in a uniform fluid at a constant speed so large that the flow seen in the body-fixed frame is steady and unseparated. The theorem relates the lift generated by an airfoil to the speed of the airfoil through the fluid, the density of the fluid and the circulation around the airfoil. The circulation is defined as the line integral around a closed loop enclosing the airfoil of the component of the velocity of the fluid tangent to the loop. It is named after Martin Kutta and Nikolai Zhukovsky who first developed its key ideas in the early 20th century. Kutta–Joukowski theorem is an inviscid theory, but it is a good approximation for real viscous flow in typical aerodynamic applications.

In fluid dynamics, the Reynolds number is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers, flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow. These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation.
The multiphase particle-in-cell method (MP-PIC) is a numerical method for modeling particle-fluid and particle-particle interactions in a computational fluid dynamics (CFD) calculation. The MP-PIC method achieves greater stability than its particle-in-cell predecessor by simultaneously treating the solid particles as computational particles and as a continuum. In the MP-PIC approach, the particle properties are mapped from the Lagrangian coordinates to an Eulerian grid through the use of interpolation functions. After evaluation of the continuum derivative terms, the particle properties are mapped back to the individual particles. This method has proven to be stable in dense particle flows, computationally efficient, and physically accurate. This has allowed the MP-PIC method to be used as particle-flow solver for the simulation of industrial-scale chemical processes involving particle-fluid flows.
In fluid dynamics, the Basset–Boussinesq–Oseen equation describes the motion of – and forces on – a small particle in unsteady flow at low Reynolds numbers. The equation is named after Joseph Valentin Boussinesq, Alfred Barnard Basset and Carl Wilhelm Oseen.

A jet mill grinds materials by using a high speed jet of compressed air or inert gas to impact particles into each other. Jet mills can be designed to output particles below a certain size while continuing to mill particles above that size, resulting in a narrow size distribution of the resulting product. Particles leaving the mill can be separated from the gas stream by cyclonic separation.