
Genetic programming (GP) is an evolutionary algorithm, an artificial intelligence technique mimicking natural evolution, which operates on a population of programs. It applies the genetic operators selection according to a predefined fitness measure, mutation and crossover.

In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems via biologically inspired operators such as selection, crossover, and mutation. Some examples of GA applications include optimizing decision trees for better performance, solving sudoku puzzles, hyperparameter optimization, and causal inference.

Evolutionary algorithms (EA) reproduce essential elements of the biological evolution in a computer algorithm in order to solve “difficult” problems, at least approximately, for which no exact or satisfactory solution methods are known. They belong to the class of metaheuristics and are a subset of population based bio-inspired algorithms and evolutionary computation, which itself are part of the field of computational intelligence. The mechanisms of biological evolution that an EA mainly imitates are reproduction, mutation, recombination and selection. Candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions (see also loss function). Evolution of the population then takes place after the repeated application of the above operators.

Evolutionary computation from computer science is a family of algorithms for global optimization inspired by biological evolution, and the subfield of artificial intelligence and soft computing studying these algorithms. In technical terms, they are a family of population-based trial and error problem solvers with a metaheuristic or stochastic optimization character.
NeuroEvolution of Augmenting Topologies (NEAT) is a genetic algorithm (GA) for the generation of evolving artificial neural networks developed by Kenneth Stanley and Risto Miikkulainen in 2002 while at The University of Texas at Austin. It alters both the weighting parameters and structures of networks, attempting to find a balance between the fitness of evolved solutions and their diversity. It is based on applying three key techniques: tracking genes with history markers to allow crossover among topologies, applying speciation to preserve innovations, and developing topologies incrementally from simple initial structures ("complexifying").

A fitness function is a particular type of objective or cost function that is used to summarize, as a single figure of merit, how close a given candidate solution is to achieving the set aims. It is an important component of evolutionary algorithms (EA), such as genetic programming, evolution strategies or genetic algorithms. An EA is a metaheuristic that reproduces the basic principles of biological evolution as a computer algorithm in order to solve challenging optimization or planning tasks, at least approximately. For this purpose, many candidate solutions are generated, which are evaluated using a fitness function in order to guide the evolutionary development towards the desired goal. Similar quality functions are also used in other metaheuristics, such as ant colony optimization or particle swarm optimization.

Crossover in evolutionary algorithms and evolutionary computation, also called recombination, is a genetic operator used to combine the genetic information of two parents to generate new offspring. It is one way to stochastically generate new solutions from an existing population, and is analogous to the crossover that happens during sexual reproduction in biology. New solutions can also be generated by cloning an existing solution, which is analogous to asexual reproduction. Newly generated solutions may be mutated before being added to the population. The aim of recombination is to transfer good characteristics from two different parents to one child.

Mutation is a genetic operator used to maintain genetic diversity of the chromosomes of a population of an evolutionary algorithm (EA), including genetic algorithms in particular. It is analogous to biological mutation.
Interactive evolutionary computation (IEC) or aesthetic selection is a general term for methods of evolutionary computation that use human evaluation. Usually human evaluation is necessary when the form of fitness function is not known or the result of optimization should fit a particular user preference.

Evolution strategy (ES) from computer science is a subclass of evolutionary algorithms, which serves as an optimization technique. It uses the major genetic operators mutation, recombination and selection of parents.

Gene expression programming (GEP) in computer programming is an evolutionary algorithm that creates computer programs or models. These computer programs are complex tree structures that learn and adapt by changing their sizes, shapes, and composition, much like a living organism. And like living organisms, the computer programs of GEP are also encoded in simple linear chromosomes of fixed length. Thus, GEP is a genotype–phenotype system, benefiting from a simple genome to keep and transmit the genetic information and a complex phenotype to explore the environment and adapt to it.

Selection is a genetic operator in an evolutionary algorithm (EA). An EA is a metaheuristic inspired by biological evolution and aims to solve challenging problems at least approximately. Selection has a dual purpose: on the one hand, it can choose individual genomes from a population for subsequent breeding. In addition, selection mechanisms are also used to choose candidate solutions (individuals) for the next generation. The biological model is natural selection.

In natural evolution and artificial evolution the fitness of a schema is rescaled to give its effective fitness which takes into account crossover and mutation.

Premature convergence is an unwanted effect in evolutionary algorithms (EA), a metaheuristic that mimics the basic principles of biological evolution as a computer algorithm for solving an optimization problem. The effect means that the population of an EA has converged too early, resulting in being suboptimal. In this context, the parental solutions, through the aid of genetic operators, are not able to generate offspring that are superior to, or outperform, their parents. Premature convergence is a common problem found in evolutionary algorithms, as it leads to a loss, or convergence of, a large number of alleles, subsequently making it very difficult to search for a specific gene in which the alleles were present. An allele is considered lost if, in a population, a gene is present, where all individuals are sharing the same value for that particular gene. An allele is, as defined by De Jong, considered to be a converged allele, when 95% of a population share the same value for a certain gene.

In computer science and operations research, a memetic algorithm (MA) is an extension of an evolutionary algorithm (EA) that aims to accelerate the evolutionary search for the optimum. An EA is a metaheuristic that reproduces the basic principles of biological evolution as a computer algorithm in order to solve challenging optimization or planning tasks, at least approximately. An MA uses one or more suitable heuristics or local search techniques to improve the quality of solutions generated by the EA and to speed up the search. The effects on the reliability of finding the global optimum depend on both the use case and the design of the MA.

Cultural algorithms (CA) are a branch of evolutionary computation where there is a knowledge component that is called the belief space in addition to the population component. In this sense, cultural algorithms can be seen as an extension to a conventional genetic algorithm. Cultural algorithms were introduced by Reynolds (see references).
In computer science and operations research, the bees algorithm is a population-based search algorithm which was developed by Pham, Ghanbarzadeh et al. in 2005. It mimics the food foraging behaviour of honey bee colonies. In its basic version the algorithm performs a kind of neighbourhood search combined with global search, and can be used for both combinatorial optimization and continuous optimization. The only condition for the application of the bees algorithm is that some measure of distance between the solutions is defined. The effectiveness and specific abilities of the bees algorithm have been proven in a number of studies.
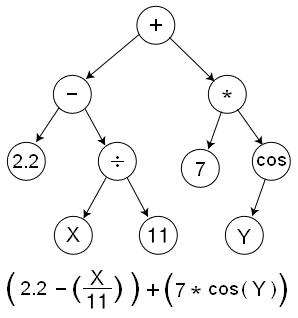
Symbolic regression (SR) is a type of regression analysis that searches the space of mathematical expressions to find the model that best fits a given dataset, both in terms of accuracy and simplicity.

The Fly Algorithm is a computational method within the field of evolutionary algorithms, designed for direct exploration of 3D spaces in applications such as computer stereo vision, robotics, and medical imaging. Unlike traditional image-based stereovision, which relies on matching features to construct 3D information, the Fly Algorithm operates by generating a 3D representation directly from random points, termed "flies." Each fly is a coordinate in 3D space, evaluated for its accuracy by comparing its projections in a scene. By iteratively refining the positions of flies based on fitness criteria, the algorithm can construct an optimized spatial representation. The Fly Algorithm has expanded into various fields, including applications in digital art, where it is used to generate complex visual patterns.

The population model of an evolutionary algorithm (EA) describes the structural properties of its population to which its members are subject. A population is the set of all proposed solutions of an EA considered in one iteration, which are also called individuals according to the biological role model. The individuals of a population can generate further individuals as offspring with the help of the genetic operators of the procedure.


