Related Research Articles

Euclid was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the Elements treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics.

The history of mathematics deals with the origin of discoveries in mathematics and the mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. From 3000 BC the Mesopotamian states of Sumer, Akkad and Assyria, followed closely by Ancient Egypt and the Levantine state of Ebla began using arithmetic, algebra and geometry for purposes of taxation, commerce, trade and also in the field of astronomy to record time and formulate calendars.

Robert Simson was a Scottish mathematician and professor of mathematics at the University of Glasgow. The Simson line is named after him.

John Playfair FRSE, FRS was a Church of Scotland minister, remembered as a scientist and mathematician, and a professor of natural philosophy at the University of Edinburgh. He is best known for his book Illustrations of the Huttonian Theory of the Earth (1802), which summarised the work of James Hutton. It was through this book that Hutton's principle of uniformitarianism, later taken up by Charles Lyell, first reached a wide audience. Playfair's textbook Elements of Geometry made a brief expression of Euclid's parallel postulate known now as Playfair's axiom.

The Elements is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid c. 300 BC. It is a collection of definitions, postulates, propositions, and mathematical proofs of the propositions. The books cover plane and solid Euclidean geometry, elementary number theory, and incommensurable lines. Elements is the oldest extant large-scale deductive treatment of mathematics. It has proven instrumental in the development of logic and modern science, and its logical rigor was not surpassed until the 19th century.
In mathematics, racks and quandles are sets with binary operations satisfying axioms analogous to the Reidemeister moves used to manipulate knot diagrams.

Alexander Bogomolny was a Soviet-born Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow Institute of Electronics and Mathematics, senior instructor at Hebrew University and software consultant at Ben Gurion University. He wrote extensively about arithmetic, probability, algebra, geometry, trigonometry and mathematical games.

Alexandre Aleksandrovich Kirilloff is a Soviet and Russian mathematician, known for his works in the fields of representation theory, topological groups and Lie groups. In particular he introduced the orbit method into representation theory. He is an emeritus professor at the University of Pennsylvania.

Robin Cope Hartshorne is an American mathematician who is known for his work in algebraic geometry.

A treatise is a formal and systematic written discourse on some subject concerned with investigating or exposing the principles of the subject and its conclusions. A monograph is a treatise on a specialized topic.

John Colin Stillwell is an Australian mathematician on the faculties of the University of San Francisco and Monash University.
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant. An invertible link is the link equivalent of an invertible knot.

Knots have been used for basic purposes such as recording information, fastening and tying objects together, for thousands of years. The early significant stimulus in knot theory would arrive later with Sir William Thomson and his vortex theory of the atom.

Infinity is something which is boundless, endless, or larger than any natural number. It is denoted by , the infinity symbol.

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.

Optics is a work on the geometry of vision written by the Greek mathematician Euclid around 300 BC. The earliest surviving manuscript of Optics is in Greek and dates from the 10th century AD.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
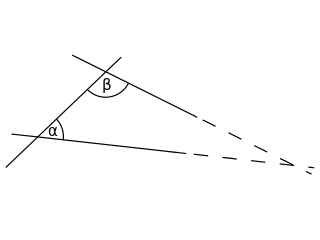
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

Noam Nisan is an Israeli computer scientist, a professor of computer science at the Hebrew University of Jerusalem. He is known for his research in computational complexity theory and algorithmic game theory.
References
- 1 2 Elhamdadi, Mohamed; Nelson, Sam (2015), Quandles, Student Mathematical Library, vol. 74, American Mathematical Society, p. vii, ISBN 9781470422134
- ↑ Barrow-Green, June (May 2006), "'Much necessary for all sortes of men': 450 years of Euclid's Elements in English", BSHM Bulletin: Journal of the British Society for the History of Mathematics, 21 (1): 2–25, doi:10.1080/17498430600566527
- ↑ Kiernan, Jim (July 2007), "David Joyce's Website", Convergence, Mathematical Association of America, retrieved 2025-01-05
- ↑ "Emeriti Faculty", Mathematics People, Clark University, retrieved 2025-01-05
- ↑ David E. Joyce at the Mathematics Genealogy Project
- ↑ Stupel, Moshe; Farhat, Mtanes; Jahangiri, Jay (June 2023), "Revisiting proof without words using color coding" (PDF), Resonance, 28 (6), Indian Academy of Sciences: 975–983, doi:10.1007/s12045-023-1626-0