
Deformation is the rate of change of shape of fluid bodies. Meteorologically, this quantity is very important in the formation of atmospheric fronts, in the explanation of cloud shapes, and in the diffusion of materials and properties. [1]

Deformation is the rate of change of shape of fluid bodies. Meteorologically, this quantity is very important in the formation of atmospheric fronts, in the explanation of cloud shapes, and in the diffusion of materials and properties. [1]
The deformation of horizontal wind is defined as , where and , representing the derivatives of wind component. Because these derivatives vary greatly with the rotation of the coordinate system, so do and . [1]
The deformation elements and (above) can be used to find the direction of the dilatation axis, the line along which the material elements stretch (also known as the stretching direction). Several flow patterns are characteristic of large deformation: confluence, diffluence, and shear flow. Confluence, also known as stretching, is the elongating of a fluid body along the flow (streamline convergence). Diffluence, also known as shearing, is the elongating of a fluid body normal to the flow (streamline divergence). [1]

Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century.
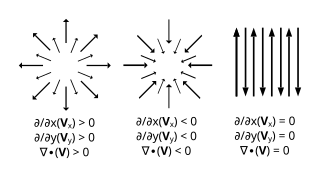
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.

In physics, the Navier–Stokes equations are certain partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In vector calculus and physics, a vector field is an assignment of a vector to each point in a subset of space. For instance, a vector field in the plane can be visualised as a collection of arrows with a given magnitude and direction, each attached to a point in the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout space, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point.

Streamlines, streaklines and pathlines are field lines in a fluid flow. They differ only when the flow changes with time, that is, when the flow is not steady. Considering a velocity vector field in three-dimensional space in the framework of continuum mechanics, we have that:

The stream function is defined for incompressible (divergence-free) flows in two dimensions – as well as in three dimensions with axisymmetry. The flow velocity components can be expressed as the derivatives of the scalar stream function. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. The two-dimensional Lagrange stream function was introduced by Joseph Louis Lagrange in 1781. The Stokes stream function is for axisymmetrical three-dimensional flow, and is named after George Gabriel Stokes.

In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition. The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.
In continuum mechanics, the material derivative describes the time rate of change of some physical quantity of a material element that is subjected to a space-and-time-dependent macroscopic velocity field. The material derivative can serve as a link between Eulerian and Lagrangian descriptions of continuum deformation.
Frontogenesis is a meteorological process of tightening of horizontal temperature gradients to produce fronts. In the end, two types of fronts form: cold fronts and warm fronts. A cold front is a narrow line where temperature decreases rapidly. A warm front is a narrow line of warmer temperatures and essentially where much of the precipitation occurs. Frontogenesis occurs as a result of a developing baroclinic wave. According to Hoskins & Bretherton, there are eight mechanisms that influence temperature gradients: horizontal deformation, horizontal shearing, vertical deformation, differential vertical motion, latent heat release, surface friction, turbulence and mixing, and radiation. Semigeostrophic frontogenesis theory focuses on the role of horizontal deformation and shear.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.
In materials science, strain rate is the change in strain (deformation) of a material with respect to time.
In physical oceanography and fluid dynamics, the wind stress is the shear stress exerted by the wind on the surface of large bodies of water – such as oceans, seas, estuaries and lakes. Stress is the quantity that describes the magnitude of a force that is causing a deformation of an object. Therefore, stress is defined as the force per unit area and its SI unit is the Pascal. When the deforming force acts parallel to the object's surface, this force is called a shear force and the stress it causes is called a shear stress. When wind is blowing over a water surface, the wind applies a wind force on the water surface. The wind stress is the component of this wind force that is parallel to the surface per unit area. Also, the wind stress can be described as the flux of horizontal momentum applied by the wind on the water surface. The wind stress causes a deformation of the water body whereby wind waves are generated. Also, the wind stress drives ocean currents and is therefore an important driver of the large-scale ocean circulation. The wind stress is affected by the wind speed, the shape of the wind waves and the atmospheric stratification. It is one of the components of the air–sea interaction, with others being the atmospheric pressure on the water surface, as well as the exchange of energy and mass between the water and the atmosphere.
In meteorology the Ellrod index is a technique for forecasting clear-air turbulence. It is calculated based on the product of horizontal deformation and vertical wind shear derived from numerical model forecast winds aloft. The deformation predictors are calculated using following information.

Boundary currents are ocean currents with dynamics determined by the presence of a coastline, and fall into two distinct categories: western boundary currents and eastern boundary currents.

In physics, deformation is the continuum mechanics transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.
Ocean dynamics define and describe the motion of water within the oceans. Ocean temperature and motion fields can be separated into three distinct layers: mixed (surface) layer, upper ocean, and deep ocean.

In fluid dynamics, hydrodynamic stability is the field which analyses the stability and the onset of instability of fluid flows. The study of hydrodynamic stability aims to find out if a given flow is stable or unstable, and if so, how these instabilities will cause the development of turbulence. The foundations of hydrodynamic stability, both theoretical and experimental, were laid most notably by Helmholtz, Kelvin, Rayleigh and Reynolds during the nineteenth century. These foundations have given many useful tools to study hydrodynamic stability. These include Reynolds number, the Euler equations, and the Navier–Stokes equations. When studying flow stability it is useful to understand more simplistic systems, e.g. incompressible and inviscid fluids which can then be developed further onto more complex flows. Since the 1980s, more computational methods are being used to model and analyse the more complex flows.

In continuum mechanics, the strain-rate tensor or rate-of-strain tensor is a physical quantity that describes the rate of change of the deformation of a material in the neighborhood of a certain point, at a certain moment of time. It can be defined as the derivative of the strain tensor with respect to time, or as the symmetric component of the Jacobian matrix of the flow velocity. In fluid mechanics it also can be described as the velocity gradient, a measure of how the velocity of a fluid changes between different points within the fluid. Though the term can refer to the differences in velocity between layers of flow in a pipe, it is often used to mean the gradient of a flow's velocity with respect to its coordinates. The concept has implications in a variety of areas of physics and engineering, including magnetohydrodynamics, mining and water treatment.
The Reynolds Equation is a partial differential equation governing the pressure distribution of thin viscous fluid films in lubrication theory. It should not be confused with Osborne Reynolds' other namesakes, Reynolds number and Reynolds-averaged Navier–Stokes equations. It was first derived by Osborne Reynolds in 1886. The classical Reynolds Equation can be used to describe the pressure distribution in nearly any type of fluid film bearing; a bearing type in which the bounding bodies are fully separated by a thin layer of liquid or gas.