
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals.

In telecommunications, orthogonal frequency-division multiplexing (OFDM) is a type of digital transmission used in digital modulation for encoding digital (binary) data on multiple carrier frequencies. OFDM has developed into a popular scheme for wideband digital communication, used in applications such as digital television and audio broadcasting, DSL internet access, wireless networks, power line networks, and 4G/5G mobile communications.
In radio communication, multipath is the propagation phenomenon that results in radio signals reaching the receiving antenna by two or more paths. Causes of multipath include atmospheric ducting, ionospheric reflection and refraction, and reflection from water bodies and terrestrial objects such as mountains and buildings. When the same signal is received over more than one path, it can create interference and phase shifting of the signal. Destructive interference causes fading; this may cause a radio signal to become too weak in certain areas to be received adequately. For this reason, this effect is also known as multipath interference or multipath distortion.

In wireless communications, fading is the variation of signal attenuation over variables like time, geographical position, and radio frequency. Fading is often modeled as a random process. In wireless systems, fading may either be due to multipath propagation, referred to as multipath-induced fading, weather, or shadowing from obstacles affecting the wave propagation, sometimes referred to as shadow fading.

The short-time Fourier transform (STFT) is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. In practice, the procedure for computing STFTs is to divide a longer time signal into shorter segments of equal length and then compute the Fourier transform separately on each shorter segment. This reveals the Fourier spectrum on each shorter segment. One then usually plots the changing spectra as a function of time, known as a spectrogram or waterfall plot, such as commonly used in software defined radio (SDR) based spectrum displays. Full bandwidth displays covering the whole range of an SDR commonly use fast Fourier transforms (FFTs) with 2^24 points on desktop computers.

In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy.
In pulsed radar and sonar signal processing, an ambiguity function is a two-dimensional function of propagation delay and Doppler frequency , . It represents the distortion of a returned pulse due to the receiver matched filter of the return from a moving target. The ambiguity function is defined by the properties of the pulse and of the filter, and not any particular target scenario.
In probability theory and statistics, given a stochastic process, the autocovariance is a function that gives the covariance of the process with itself at pairs of time points. Autocovariance is closely related to the autocorrelation of the process in question.

In optics, various autocorrelation functions can be experimentally realized. The field autocorrelation may be used to calculate the spectrum of a source of light, while the intensity autocorrelation and the interferometric autocorrelation are commonly used to estimate the duration of ultrashort pulses produced by modelocked lasers. The laser pulse duration cannot be easily measured by optoelectronic methods, since the response time of photodiodes and oscilloscopes are at best of the order of 200 femtoseconds, yet laser pulses can be made as short as a few femtoseconds.
Directional statistics is the subdiscipline of statistics that deals with directions, axes or rotations in Rn. More generally, directional statistics deals with observations on compact Riemannian manifolds including the Stiefel manifold.
A cyclostationary process is a signal having statistical properties that vary cyclically with time. A cyclostationary process can be viewed as multiple interleaved stationary processes. For example, the maximum daily temperature in New York City can be modeled as a cyclostationary process: the maximum temperature on July 21 is statistically different from the temperature on December 20; however, it is a reasonable approximation that the temperature on December 20 of different years has identical statistics. Thus, we can view the random process composed of daily maximum temperatures as 365 interleaved stationary processes, each of which takes on a new value once per year.
Grating-eliminated no-nonsense observation of ultrafast incident laser light e-fields (GRENOUILLE) is an ultrashort pulse measurement technique based on frequency-resolved optical gating (FROG). The acronym was chosen because of the technique's relationship to FROG; grenouille is French for frog.

The Wigner distribution function (WDF) is used in signal processing as a transform in time-frequency analysis.
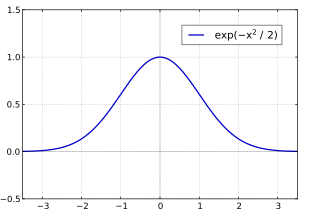
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window function, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal x(t) is defined by this formula:
Bilinear time–frequency distributions, or quadratic time–frequency distributions, arise in a sub-field of signal analysis and signal processing called time–frequency signal processing, and, in the statistical analysis of time series data. Such methods are used where one needs to deal with a situation where the frequency composition of a signal may be changing over time; this sub-field used to be called time–frequency signal analysis, and is now more often called time–frequency signal processing due to the progress in using these methods to a wide range of signal-processing problems.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.

As described here, white light interferometry is a non-contact optical method for surface height measurement on 3D structures with surface profiles varying between tens of nanometers and a few centimeters. It is often used as an alternative name for coherence scanning interferometry in the context of areal surface topography instrumentation that relies on spectrally-broadband, visible-wavelength light.
In quantum optics, correlation functions are used to characterize the statistical and coherence properties – the ability of waves to interfere – of electromagnetic radiation, like optical light. Higher order coherence or n-th order coherence extends the concept of coherence to quantum optics and coincidence experiments. It is used to differentiate between optics experiments that require a quantum mechanical description from those for which classical fields are sufficient.
The residence time of a fluid parcel is the total time that the parcel has spent inside a control volume (e.g.: a chemical reactor, a lake, a human body). The residence time of a set of parcels is quantified in terms of the frequency distribution of the residence time in the set, which is known as residence time distribution (RTD), or in terms of its average, known as mean residence time.
Ultra-wideband impulse radio ranging is a wireless positioning technology based on IEEE 802.15.4z standard, which is a wireless communication protocol introduced by IEEE, for systems operating in unlicensed spectrum, equipped with extremely large bandwidth transceivers. UWB enables very accurate ranging without introducing significant interference with narrowband systems. To achieve these stringent requirements, UWB-IR systems exploit the available bandwidth that they support, which guarantees very accurate timing and robustness against multipath, especially in indoor environments. The available bandwidth also enables UWB systems to spread the signal power over a large spectrum, avoiding narrowband interference.













