
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
Unsupervised learning is a method in machine learning where, in contrast to supervised learning, algorithms learn patterns exclusively from unlabeled data. Within such an approach, a machine learning model tries to find any similarities, differences, patterns, and structure in data by itself. No prior human intervention is needed.

Nonlinear dimensionality reduction, also known as manifold learning, is any of various related techniques that aim to project high-dimensional data onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis.
Global optimization is a branch of applied mathematics and numerical analysis that attempts to find the global minima or maxima of a function or a set of functions on a given set. It is usually described as a minimization problem because the maximization of the real-valued function is equivalent to the minimization of the function .
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable. Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics.
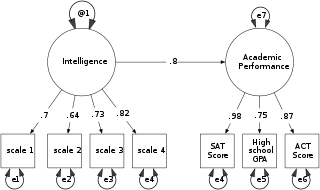
Structural equation modeling (SEM) is a diverse set of methods used by scientists doing both observational and experimental research. SEM is used mostly in the social and behavioral sciences but it is also used in epidemiology, business, and other fields. A definition of SEM is difficult without reference to technical language, but a good starting place is the name itself.
Non-negative matrix factorization, also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix V is factorized into (usually) two matrices W and H, with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms or muscular activity, non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically.

In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into sets of nodes such that each set of nodes is densely connected internally. In the particular case of non-overlapping community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But overlapping communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities. A related but different problem is community search, where the goal is to find a community that a certain vertex belongs to.
In computational physics, variational Monte Carlo (VMC) is a quantum Monte Carlo method that applies the variational method to approximate the ground state of a quantum system.

The stochastic block model is a generative model for random graphs. This model tends to produce graphs containing communities, subsets of nodes characterized by being connected with one another with particular edge densities. For example, edges may be more common within communities than between communities. Its mathematical formulation was first introduced in 1983 in the field of social network analysis by Paul W. Holland et al. The stochastic block model is important in statistics, machine learning, and network science, where it serves as a useful benchmark for the task of recovering community structure in graph data.

Blockmodeling is a set or a coherent framework, that is used for analyzing social structure and also for setting procedure(s) for partitioning (clustering) social network's units, based on specific patterns, which form a distinctive structure through interconnectivity. It is primarily used in statistics, machine learning and network science.
Aleš Žiberna is a Slovene statistician, whose specialty is network analysis. His specific research interests include blockmodeling, multivariate analysis and computer intensive methods.
In generalized blockmodeling, the blockmodeling is done by "the translation of an equivalence type into a set of permitted block types", which differs from the conventional blockmodeling, which is using the indirect approach. It's a special instance of the direct blockmodeling approach.
Generalized blockmodeling of valued networks is an approach of the generalized blockmodeling, dealing with valued networks.
In mathematics applied to analysis of social structures, homogeneity blockmodeling is an approach in blockmodeling, which is best suited for a preliminary or main approach to valued networks, when a prior knowledge about these networks is not available. This is due to the fact, that homogeneity blockmodeling emphasizes the similarity of link (tie) strengths within the blocks over the pattern of links. In this approach, tie (link) values are assumed to be equal (homogenous) within blocks.
Exploratory blockmodeling is an (inductive) approach in blockmodeling regarding the specification of an ideal blockmodel. This approach, also known as hypotheses-generating, is the simplest approach, as it "merely involves the definition of the block types permitted as well as of the number of clusters." With this approach, researcher usually defines the best possible blockmodel, which then represent the base for the analysis of the whole network.
Confirmatory blockmodeling is a deductive approach in blockmodeling, where a blockmodel is prespecify before the analysis, and then the analysis is fit to this model. When only a part of analysis is prespecify, it is called partially confirmatory blockmodeling.
Implicit blockmodeling is an approach in blockmodeling, similar to a valued and homogeneity blockmodeling, where initially an additional normalization is used and then while specifying the parameter of the relevant link is replaced by the block maximum.
Generalized blockmodeling of binary networks is an approach of generalized blockmodeling, analysing the binary network(s).




