
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a disc.

In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the International System of Units (SI) system the base unit for length is the metre.

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria. The term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects or a degree of separation. Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space.

In mathematics, a knot is an embedding of the circle into three-dimensional Euclidean space, R3. Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of R3 which takes one knot to the other.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An incidence structure is what is obtained when all other concepts are removed and all that remains is the data about which points lie on which lines. Even with this severe limitation, theorems can be proved and interesting facts emerge concerning this structure. Such fundamental results remain valid when additional concepts are added to form a richer geometry. It sometimes happens that authors blur the distinction between a study and the objects of that study, so it is not surprising to find that some authors refer to incidence structures as incidence geometries.

In classical geometry, a radius of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the Latin radius, meaning ray but also the spoke of a chariot wheel. The typical abbreviation and mathematical variable symbol for radius is R or r. By extension, the diameter D is defined as twice the radius:

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices; thus, it can be described as "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.
Proximity problems is a class of problems in computational geometry which involve estimation of distances between geometric objects.
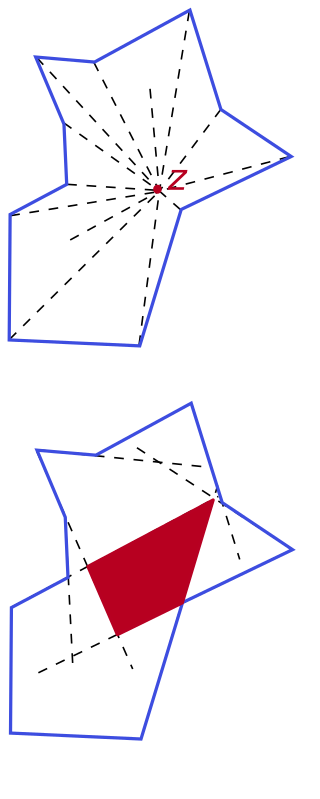
In geometry, a star-shaped polygon is a polygonal region in the plane that is a star domain, that is, a polygon that contains a point from which the entire polygon boundary is visible.

In computational geometry, the method of rotating calipers is an algorithm design technique that can be used to solve optimization problems including finding the width or diameter of a set of points.
In mathematics, the Schoenflies problem or Schoenflies theorem, of geometric topology is a sharpening of the Jordan curve theorem by Arthur Schoenflies. For Jordan curves in the plane it is often referred to as the Jordan–Schoenflies theorem.
In discrete mathematics and theoretical computer science, the flip distance between two triangulations of the same point set is the number of flips required to transform one triangulation into another. A flip removes an edge between two triangles in the triangulation and then adds the other diagonal in the edge's enclosing quadrilateral, forming a different triangulation of the same point set.
In metric geometry and computational geometry, a minimum-diameter spanning tree of a finite set of points in a metric space is a spanning tree in which the diameter is as small as possible.









