In physics, the cross section is a measure of the probability that a specific process will take place when some kind of radiant excitation intersects a localized phenomenon. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In physics, the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.

In particle physics, Rutherford scattering is the elastic scattering of charged particles by the Coulomb interaction. It is a physical phenomenon explained by Ernest Rutherford in 1911 that led to the development of the planetary Rutherford model of the atom and eventually the Bohr model. Rutherford scattering was first referred to as Coulomb scattering because it relies only upon the static electric (Coulomb) potential, and the minimum distance between particles is set entirely by this potential. The classical Rutherford scattering process of alpha particles against gold nuclei is an example of "elastic scattering" because neither the alpha particles nor the gold nuclei are internally excited. The Rutherford formula further neglects the recoil kinetic energy of the massive target nucleus.

Rayleigh scattering, named after the 19th-century British physicist Lord Rayleigh, is the predominantly elastic scattering of light, or other electromagnetic radiation, by particles with a size much smaller than the wavelength of the radiation. For light frequencies well below the resonance frequency of the scattering medium, the amount of scattering is inversely proportional to the fourth power of the wavelength, e.g., a blue color is scattered much more than a red color as light propagates through air.

The kinetic theory of gases is a simple, historically significant classical model of the thermodynamic behavior of gases, with which many principal concepts of thermodynamics were established. The model describes a gas as a large number of identical submicroscopic particles, all of which are in constant, rapid, random motion. Their size is assumed to be much smaller than the average distance between the particles. The particles undergo random elastic collisions between themselves and with the enclosing walls of the container. The basic version of the model describes the ideal gas, and considers no other interactions between the particles.
In physics, mean free path is the average distance over which a moving particle travels before substantially changing its direction or energy, typically as a result of one or more successive collisions with other particles.
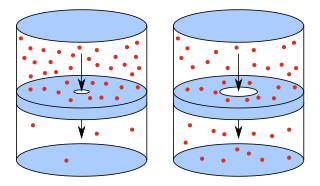
In physics and chemistry, effusion is the process in which a gas escapes from a container through a hole of diameter considerably smaller than the mean free path of the molecules. Such a hole is often described as a pinhole and the escape of the gas is due to the pressure difference between the container and the exterior. Under these conditions, essentially all molecules which arrive at the hole continue and pass through the hole, since collisions between molecules in the region of the hole are negligible. Conversely, when the diameter is larger than the mean free path of the gas, flow obeys the Sampson flow law.

Stellar dynamics is the branch of astrophysics which describes in a statistical way the collective motions of stars subject to their mutual gravity. The essential difference from celestial mechanics is that the number of body

Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is the low-energy limit of Compton scattering: the particle's kinetic energy and photon frequency do not change as a result of the scattering. This limit is valid as long as the photon energy is much smaller than the mass energy of the particle: , or equivalently, if the wavelength of the light is much greater than the Compton wavelength of the particle.
In quantum physics, the scattering amplitude is the probability amplitude of the outgoing spherical wave relative to the incoming plane wave in a stationary-state scattering process. At large distances from the centrally symmetric scattering center, the plane wave is described by the wavefunction
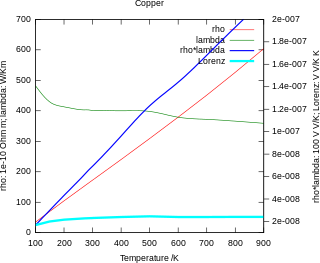
In physics, the Wiedemann–Franz law states that the ratio of the electronic contribution of the thermal conductivity (κ) to the electrical conductivity (σ) of a metal is proportional to the temperature (T).

Collision theory is a principle of chemistry used to predict the rates of chemical reactions. It states that when suitable particles of the reactant hit each other with the correct orientation, only a certain amount of collisions result in a perceptible or notable change; these successful changes are called successful collisions. The successful collisions must have enough energy, also known as activation energy, at the moment of impact to break the pre-existing bonds and form all new bonds. This results in the products of the reaction. The activation energy is often predicted using the Transition state theory. Increasing the concentration of the reactant brings about more collisions and hence more successful collisions. Increasing the temperature increases the average kinetic energy of the molecules in a solution, increasing the number of collisions that have enough energy. Collision theory was proposed independently by Max Trautz in 1916 and William Lewis in 1918.
The Loschmidt constant or Loschmidt's number (symbol: n0) is the number of particles (atoms or molecules) of an ideal gas per volume (the number density), and usually quoted at standard temperature and pressure. The 2014 CODATA recommended value is 2.6867811(15)×1025 per cubic metre at 0 °C and 1 atm and the 2006 CODATA recommended value was 2.686 7774(47)×1025 per cubic metre at 0 °C and 1 atm. It is named after the Austrian physicist Johann Josef Loschmidt, who was the first to estimate the physical size of molecules in 1865. The term "Loschmidt constant" is also sometimes used to refer to the Avogadro constant, particularly in German texts.
In condensed matter physics and crystallography, the static structure factor is a mathematical description of how a material scatters incident radiation. The structure factor is a critical tool in the interpretation of scattering patterns obtained in X-ray, electron and neutron diffraction experiments.
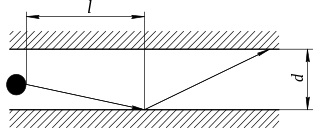
In physics, Knudsen diffusion, named after Martin Knudsen, is a means of diffusion that occurs when the scale length of a system is comparable to or smaller than the mean free path of the particles involved. An example of this is in a long pore with a narrow diameter (2–50 nm) because molecules frequently collide with the pore wall. As another example, consider the diffusion of gas molecules through very small capillary pores. If the pore diameter is smaller than the mean free path of the diffusing gas molecules, and the density of the gas is low, the gas molecules collide with the pore walls more frequently than with each other, leading to Knudsen diffusion.

In physics, absorption cross section is a measure for the probability of an absorption process. More generally, the term cross section is used in physics to quantify the probability of a certain particle-particle interaction, e.g., scattering, electromagnetic absorption, etc. Typical absorption cross section has units of cm2⋅molecule−1. In honor of the fundamental contribution of Maria Goeppert Mayer to this area, the unit for the two-photon absorption cross section is named the "GM". One GM is 10−50 cm4⋅s⋅photon−1.
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurately, the diffusion coefficient times the local concentration is the proportionality constant between the negative value of the mole fraction gradient and the molar flux. This distinction is especially significant in gaseous systems with strong temperature gradients. Diffusivity derives its definition from Fick's law and plays a role in numerous other equations of physical chemistry.
Equilibrium isotope fractionation is the partial separation of isotopes between two or more substances in chemical equilibrium. Equilibrium fractionation is strongest at low temperatures, and forms the basis of the most widely used isotopic paleothermometers : D/H and 18O/16O records from ice cores, and 18O/16O records from calcium carbonate. It is thus important for the construction of geologic temperature records. Isotopic fractionations attributed to equilibrium processes have been observed in many elements, from hydrogen (D/H) to uranium (238U/235U). In general, the light elements are most susceptible to fractionation, and their isotopes tend to be separated to a greater degree than heavier elements.
In astrophysics, the mass–luminosity relation is an equation giving the relationship between a star's mass and its luminosity, first noted by Jakob Karl Ernst Halm. The relationship is represented by the equation:
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.
















