Discontinuity layout optimization (DLO) is an engineering analysis procedure which can be used to directly establish the amount of load that can be carried by a solid or structure prior to collapse. Using DLO the layout of failure planes, or 'discontinuities', in a collapsing solid or structure are identified using mathematical optimization methods (hence the name, 'discontinuity layout optimization'). It is assumed that failure occurs in a ductile or 'plastic' manner.
The DLO procedure involves a number of steps, as outlined below.
The set of potential discontinuities can include discontinuities which crossover one another, allowing complex failure patterns to be identified (e.g. involving ‘fan’ mechanisms, where many discontinuities radiate from a point).
DLO can be formulated in terms of equilibrium relations ('static' formulation) or in terms of displacements ('kinematic' formulation). In the latter case the objective of the mathematical optimization problem is to minimize the internal energy dissipated along discontinuities, subject to nodal compatibility constraints. This can be solved using efficient linear programming techniques and, when combined with an algorithm originally developed for truss layout optimization problems, [1] it has been found that modern computer power can be used to directly search through very large numbers of different failure mechanism topologies (up to approx. 21,000,000,000 different topologies on current generation PCs). A full description of the application of DLO to plane strain problems has been provided by Smith and Gilbert, [2] to masonry arch analysis by Gilbert et al, [3] to slab problems by Gilbert et al, [4] [5] [6] and to 3D problems by Hawksbee et al, [7] and Zhang. [8]
Whereas with finite element analysis (FEM), a widely used alternative engineering analysis procedure, mathematical relations are formed for the underlying continuum mechanics problem, DLO involves analysis of a potentially much simpler discontinuum problem, with the problem being posed entirely in terms of the individual discontinuities which interconnect nodes laid out across the body under consideration. Additionally, when general purpose finite element programs are used to analyse the collapse state often relatively complex non-linear solvers are required, in contrast to the simpler linear programming solvers generally required in the case of DLO.
Compared with non-linear FEM, DLO has the following advantages and disadvantages:
Advantages
Disadvantages
DLO is perhaps most usefully applied to engineering problems where traditional hand calculations are difficult, or simplify the problem too much, but where recourse to more complex non-linear FEM is not justified. Applications include:
Geotechnical engineering, also known as geotechnics, is the branch of civil engineering concerned with the engineering behavior of earth materials. It uses the principles of soil mechanics and rock mechanics for the solution of its respective engineering problems. It also relies on knowledge of geology, hydrology, geophysics, and other related sciences.
Mechanical engineering is an engineering branch that combines engineering physics and mathematics principles with materials science to design, analyze, manufacture, and maintain mechanical systems. It is one of the oldest and broadest of the engineering branches.
Multi-disciplinary design optimization (MDO) is a field of engineering that uses optimization methods to solve design problems incorporating a number of disciplines. It is also known as multidisciplinary system design optimization (MSDO).
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem where some of the constraints or the objective function are nonlinear. An optimization problem is one of calculation of the extrema of an objective function over a set of unknown real variables and conditional to the satisfaction of a system of equalities and inequalities, collectively termed constraints. It is the sub-field of mathematical optimization that deals with problems that are not linear.
Topology optimization (TO) is a mathematical method that optimizes material layout within a given design space, for a given set of loads, boundary conditions and constraints with the goal of maximizing the performance of the system. TO is different from shape optimization and sizing optimization in the sense that the design can attain any shape within the design space, instead of dealing with predefined configurations.
Earthquake engineering is an interdisciplinary branch of engineering that designs and analyzes structures, such as buildings and bridges, with earthquakes in mind. Its overall goal is to make such structures more resistant to earthquakes. An earthquake engineer aims to construct structures that will not be damaged in minor shaking and will avoid serious damage or collapse in a major earthquake. Earthquake engineering is the scientific field concerned with protecting society, the natural environment, and the man-made environment from earthquakes by limiting the seismic risk to socio-economically acceptable levels. Traditionally, it has been narrowly defined as the study of the behavior of structures and geo-structures subject to seismic loading; it is considered as a subset of structural engineering, geotechnical engineering, mechanical engineering, chemical engineering, applied physics, etc. However, the tremendous costs experienced in recent earthquakes have led to an expansion of its scope to encompass disciplines from the wider field of civil engineering, mechanical engineering, nuclear engineering, and from the social sciences, especially sociology, political science, economics, and finance.
DLO can refer to:
The finite element method (FEM) is a powerful technique originally developed for numerical solution of complex problems in structural mechanics, and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at discrete points called nodes. Elements may have physical properties such as thickness, coefficient of thermal expansion, density, Young's modulus, shear modulus and Poisson's ratio.
A crash simulation is a virtual recreation of a destructive crash test of a car or a highway guard rail system using a computer simulation in order to examine the level of safety of the car and its occupants. Crash simulations are used by automakers during computer-aided engineering (CAE) analysis for crashworthiness in the computer-aided design (CAD) process of modelling new cars. During a crash simulation, the kinetic energy, or energy of motion, that a vehicle has before the impact is transformed into deformation energy, mostly by plastic deformation (plasticity) of the car body material, at the end of the impact.
Discontinuous deformation analysis (DDA) is a type of discrete element method (DEM) originally proposed by Shi in 1988. DDA is somewhat similar to the finite element method for solving stress-displacement problems, but accounts for the interaction of independent particles (blocks) along discontinuities in fractured and jointed rock masses. DDA is typically formulated as a work-energy method, and can be derived using the principle of minimum potential energy or by using Hamilton's principle. Once the equations of motion are discretized, a step-wise linear time marching scheme in the Newmark family is used for the solution of the equations of motion. The relation between adjacent blocks is governed by equations of contact interpenetration and accounts for friction. DDA adopts a stepwise approach to solve for the large displacements that accompany discontinuous movements between blocks. The blocks are said to be "simply deformable". Since the method accounts for the inertial forces of the blocks' mass, it can be used to solve the full dynamic problem of block motion.
A triaxial shear test is a common method to measure the mechanical properties of many deformable solids, especially soil and rock, and other granular materials or powders. There are several variations on the test.
The finite element method (FEM) is a widely used method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.
Z88 is a software package for the finite element method (FEM) and topology optimization. A team led by Frank Rieg at the University of Bayreuth started development in 1985 and now the software is used by several universities, as well as small and medium-sized enterprises. Z88 is capable of calculating two and three dimensional element types with a linear approach. The software package contains several solvers and two post-processors and is available for Microsoft Windows, Mac OS X and Unix/Linux computers in 32-bit and 64-bit versions. Benchmark tests conducted in 2007 showed a performance on par with commercial software.
Slope stability analysis is a static or dynamic, analytical or empirical method to evaluate the stability of earth and rock-fill dams, embankments, excavated slopes, and natural slopes in soil and rock. Slope stability refers to the condition of inclined soil or rock slopes to withstand or undergo movement. The stability condition of slopes is a subject of study and research in soil mechanics, geotechnical engineering and engineering geology. Analyses are generally aimed at understanding the causes of an occurred slope failure, or the factors that can potentially trigger a slope movement, resulting in a landslide, as well as at preventing the initiation of such movement, slowing it down or arresting it through mitigation countermeasures.
Extreme Loading for Structures (ELS) is commercial structural-analysis software based on the applied element method (AEM) for the automatic tracking and propagation of cracks, separation of elements, element collision, and collapse of structures under extreme loads. AEM combines features of Finite element method and Discrete element method simulation with its own solver capabilities for the generation of PC-based structural analysis.
The applied element method (AEM) is a numerical analysis used in predicting the continuum and discrete behavior of structures. The modeling method in AEM adopts the concept of discrete cracking allowing it to automatically track structural collapse behavior passing through all stages of loading: elastic, crack initiation and propagation in tension-weak materials, reinforcement yield, element separation, element contact and collision, as well as collision with the ground and adjacent structures.
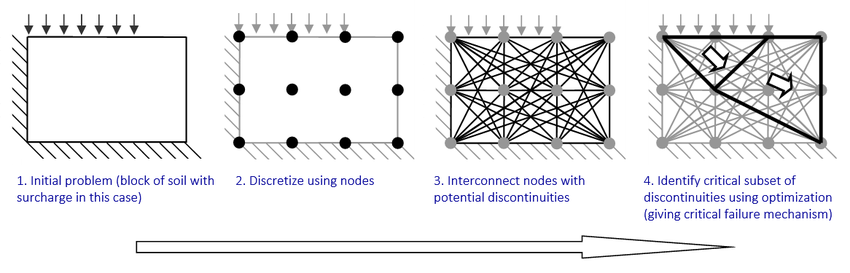
A finite element limit analysis (FELA) uses optimisation techniques to directly compute the upper or lower bound plastic collapse load for a mechanical system rather than time stepping to a collapse load, as might be undertaken with conventional non-linear finite element techniques. The problem may be formulated in either a kinematic or equilibrium form.
Smoothed finite element methods (S-FEM) are a particular class of numerical simulation algorithms for the simulation of physical phenomena. It was developed by combining meshfree methods with the finite element method. S-FEM are applicable to solid mechanics as well as fluid dynamics problems, although so far they have mainly been applied to the former.
The Newmark's sliding block analysis method is an engineering that calculates permanent displacements of soil slopes during seismic loading. Newmark analysis does not calculate actual displacement, but rather is an index value that can be used to provide an indication of the structures likelihood of failure during a seismic event. It is also simply called Newmark's analysis or Sliding block method of slope stability analysis.
Limit analysis is a structural analysis field which is dedicated to the development of efficient methods to directly determine estimates of the collapse load of a given structural model without resorting to iterative or incremental analysis. For this purpose, the field of limit analysis is based on a set of theorems, referred to as limit theorems, which are a set of theorems based on the law of conservation of energy that state properties regarding stresses and strains, lower and upper-bound limits for the collapse load and the exact collapse load.