
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable , or just distribution function of , evaluated at , is the probability that will take a value less than or equal to .
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

In mathematics, the Dirac delta function, also known as the unit impulse symbol, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. It can also be interpreted as a linear functional that maps every function to its value at zero, or as the weak limit of a sequence of bump functions, which are zero over most of the real line, with a tall spike at the origin. Bump functions are thus sometimes called "approximate" or "nascent" delta functions.
Within economics, the concept of utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness within the theory of utilitarianism by moral philosophers such as Jeremy Bentham and John Stuart Mill. The term has been adapted and reapplied within neoclassical economics, which dominates modern economic theory, as a utility function that represents a single consumer's preference ordering over a choice set but is not comparable across consumers. This concept of utility is personal and is based on choice rather than on the pleasure received, and so is more rigorously specified than the original concept but makes it less useful for ethical decisions.
Distributions, also known as Schwartz distributions or generalized functions, are objects that generalize the classical notion of functions in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative. Distributions are widely used in the theory of partial differential equations, where it may be easier to establish the existence of distributional solutions than classical solutions, or where appropriate classical solutions may not exist. Distributions are also important in physics and engineering where many problems naturally lead to differential equations whose solutions or initial conditions are distributions, such as the Dirac delta function.
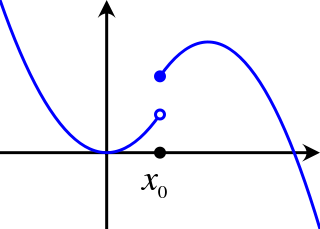
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemi-continuous at a point if, roughly speaking, the function values for arguments near are not much higher than

In mathematics, the Wiener process is a real valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown. It is one of the best known Lévy processes and occurs frequently in pure and applied mathematics, economics, quantitative finance, evolutionary biology, and physics.

The time value of money is the widely accepted conjecture that there is greater benefit to receiving a sum of money now rather than an identical sum later. It may be seen as an implication of the later-developed concept of time preference.
In mathematics, a function space is a set of functions between two fixed sets. Often, the domain and/or codomain will have additional structure which is inherited by the function space. For example, the set of functions from any set X into a vector space has a natural vector space structure given by pointwise addition and scalar multiplication. In other scenarios, the function space might inherit a topological or metric structure, hence the name function space.
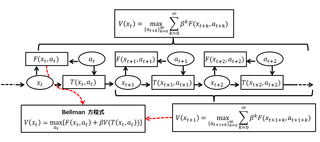
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes.

In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives it has over some domain. At the very minimum, a function could be considered smooth if it is differentiable everywhere. At the other end, it might also possess derivatives of all orders in its domain, in which case it is said to be infinitely differentiable and referred to as a C-infinity function.
In economics, discounted utility is the utility (desirability) of some future event, such as consuming a certain amount of a good, as perceived at the present time as opposed to at the time of its occurrence. It is calculated as the present discounted value of future utility, and for people with time preference for sooner rather than later gratification, it is less than the future utility. The utility of an event x occurring at future time t under utility function u, discounted back to the present using discount factor Is
In economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time. Formally, exponential discounting occurs when total utility is given by
The Ramsey–Cass–Koopmans model, or Ramsey growth model, is a neoclassical model of economic growth based primarily on the work of Frank P. Ramsey, with significant extensions by David Cass and Tjalling Koopmans. The Ramsey–Cass–Koopmans model differs from the Solow–Swan model in that the choice of consumption is explicitly microfounded at a point in time and so endogenizes the savings rate. As a result, unlike in the Solow–Swan model, the saving rate may not be constant along the transition to the long run steady state. Another implication of the model is that the outcome is Pareto optimal or Pareto efficient.
Merton's portfolio problem is a well known problem in continuous-time finance and in particular intertemporal portfolio choice. An investor must choose how much to consume and must allocate his wealth between stocks and a risk-free asset so as to maximize expected utility. The problem was formulated and solved by Robert C. Merton in 1969 both for finite lifetimes and for the infinite case. Research has continued to extend and generalize the model to include factors like transaction costs and bankruptcy.
Consumption smoothing is the economic concept used to express the desire of people to have a stable path of consumption. People desire to translate their consumption from periods of high income to periods of low income to obtain more stability and predictability. There exist many states of the world, which means there are many possible outcomes that can occur throughout an individual's life. Therefore, to reduce the uncertainty that occurs, people choose to give up some consumption today to prevent against an adverse outcome in the future. In order for one to adequately and properly prepare for unforeseen circumstances that can occur in the future, we must start planning today, putting money aside for when these unforeseen circumstances happen.
In actuarial science and applied probability, ruin theory uses mathematical models to describe an insurer's vulnerability to insolvency/ruin. In such models key quantities of interest are the probability of ruin, distribution of surplus immediately prior to ruin and deficit at time of ruin.
In macroeconomics, the cost of business cycles is the decrease in social welfare, if any, caused by business cycle fluctuations.
In mathematics, , the vector space of bounded sequences with the supremum norm, and , the vector space of essentially bounded measurable functions with the essential supremum norm, are two closely related Banach spaces. In fact the former is a special case of the latter. As a Banach space they are the continuous dual of the Banach spaces of absolutely summable sequences, and of absolutely integrable measurable functions. Pointwise multiplication gives them the structure of a Banach algebra, and in fact they are the standard examples of abelian Von Neumann algebras.
In economics, the Debreu theorems are several statements about the representation of a preference ordering by a real-valued function. The theorems were proved by Gerard Debreu during the 1950s.












