In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings.

In economics, an indifference curve connects points on a graph representing different quantities of two goods, points between which a consumer is indifferent. That is, any combinations of two products indicated by the curve will provide the consumer with equal levels of utility, and the consumer has no preference for one combination or bundle of goods over a different combination on the same curve. One can also refer to each point on the indifference curve as rendering the same level of utility (satisfaction) for the consumer. In other words, an indifference curve is the locus of various points showing different combinations of two goods providing equal utility to the consumer. Utility is then a device to represent preferences rather than something from which preferences come. The main use of indifference curves is in the representation of potentially observable demand patterns for individual consumers over commodity bundles.
Marginalism is a theory of economics that attempts to explain the discrepancy in the value of goods and services by reference to their secondary, or marginal, utility. It states that the reason why the price of diamonds is higher than that of water, for example, owes to the greater additional satisfaction of the diamonds over the water. Thus, while the water has greater total utility, the diamond has greater marginal utility.

The theory of consumer choice is the branch of microeconomics that relates preferences to consumption expenditures and to consumer demand curves. It analyzes how consumers maximize the desirability of their consumption, by maximizing utility subject to a consumer budget constraint. Factors influencing consumers' evaluation of the utility of goods include: income level, cultural factors, product information and physio-psychological factors.
In behavioral economics, time preference is the current relative valuation placed on receiving a good at an earlier date compared with receiving it at a later date. Applications for these preferences include finance, health, climate change.
In economics, hyperbolic discounting is a time-inconsistent model of delay discounting. It is one of the cornerstones of behavioral economics and its brain-basis is actively being studied by neuroeconomics researchers.
In economics, a discount function is used in economic models to describe the weights placed on rewards received at different points in time. For example, if time is discrete and utility is time-separable, with the discount function f(t) having a negative first derivative and with ct (or c(t) in continuous time) defined as consumption at time t, total utility from an infinite stream of consumption is given by:
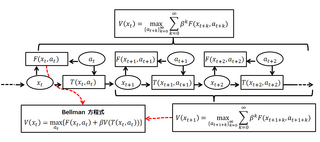
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.
In economics, dynamic inconsistency or time inconsistency is a situation in which a decision-maker's preferences change over time in such a way that a preference can become inconsistent at another point in time. This can be thought of as there being many different "selves" within decision makers, with each "self" representing the decision-maker at a different point in time; the inconsistency occurs when not all preferences are aligned.
In economics, discounted utility is the utility (desirability) of some future event, such as consuming a certain amount of a good, as perceived at the present time as opposed to at the time of its occurrence. It is calculated as the present discounted value of future utility, and for people with time preference for sooner rather than later gratification, it is less than the future utility. The utility of an event x occurring at future time t under utility function u, discounted back to the present using discount factor β, is
Social discount rate (SDR) is the discount rate used in computing the value of funds spent on social projects. Discount rates are used to put a present value on costs and benefits that will occur at a later date. Determining this rate is not always easy and can be the subject of discrepancies in the true net benefit to certain projects, plans and policies. The discount rate is considered as a critical element in cost–benefit analysis when the costs and the benefits differ in their distribution over time, this usually occurs when the project that is being studied is over a long period of time.
The Ramsey–Cass–Koopmans model, or Ramsey growth model, is a neoclassical model of economic growth based primarily on the work of Frank P. Ramsey in 1928, with significant extensions by David Cass and Tjalling Koopmans in 1965. The Ramsey–Cass–Koopmans model differs from the Solow–Swan model in that the choice of consumption is explicitly microfounded at a point in time and so endogenizes the savings rate. As a result, unlike in the Solow–Swan model, the saving rate may not be constant along the transition to the long run steady state. Another implication of the model is that the outcome is Pareto optimal or Pareto efficient.
In economics, Epstein–Zin preferences refers to a specification of recursive utility.
Consumption smoothing is an economic concept for the practice of optimizing a person's standard of living through an appropriate balance between savings and consumption over time. An optimal consumption rate should be relatively similar at each stage of a person's life rather than fluctuate wildly. Luxurious consumption at an old age does not compensate for an impoverished existence at other stages in one's life.
In stochastic calculus, the Doléans-Dade exponential or stochastic exponential of a semimartingale X is the unique strong solution of the stochastic differential equation where denotes the process of left limits, i.e., .

In economics, the isoelastic function for utility, also known as the isoelastic utility function, or power utility function, is used to express utility in terms of consumption or some other economic variable that a decision-maker is concerned with. The isoelastic utility function is a special case of hyperbolic absolute risk aversion and at the same time is the only class of utility functions with constant relative risk aversion, which is why it is also called the CRRA utility function. In statistics, the same function is called the Box-Cox transformation.
Marginal utility, in mainstream economics, describes the change in utility of one unit of a good or service. Marginal utility can be positive, negative, or zero. Negative marginal utility implies that every consumed additional unit of a commodity causes more harm than good, leading to a decrease in overall utility. In contrast, positive marginal utility indicates that every additional unit consumed increases overall utility.
In finance, economics, and decision theory, hyperbolic absolute risk aversion (HARA) refers to a type of risk aversion that is particularly convenient to model mathematically and to obtain empirical predictions from. It refers specifically to a property of von Neumann–Morgenstern utility functions, which are typically functions of final wealth, and which describe a decision-maker's degree of satisfaction with the outcome for wealth. The final outcome for wealth is affected both by random variables and by decisions. Decision-makers are assumed to make their decisions so as to maximize the expected value of the utility function.
Intertemporal portfolio choice is the process of allocating one's investable wealth to various assets, especially financial assets, repeatedly over time, in such a way as to optimize some criterion. The set of asset proportions at any time defines a portfolio. Since the returns on almost all assets are not fully predictable, the criterion has to take financial risk into account. Typically the criterion is the expected value of some concave function of the value of the portfolio after a certain number of time periods—that is, the expected utility of final wealth. Alternatively, it may be a function of the various levels of goods and services consumption that are attained by withdrawing some funds from the portfolio after each time period.
Ergodicity economics is a research programme that applies the concept of ergodicity to problems in economics and decision-making under uncertainty. The programme's main goal is to understand how traditional economic theory, framed in terms of the expectation values, changes when replacing expectation value with time averages. In particular, the programme is interested in understanding how behaviour is shaped by non-ergodic economic processes, that is processes where the expectation value of an observable does not equal its time average.





