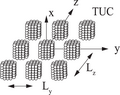
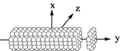
In the discrete dipole approximation, a target object is represented as a finite array of N point dipoles located at positions  (
( ). The polarization vector
). The polarization vector  of each dipole is related to the local electric field
of each dipole is related to the local electric field  at that dipole by its polarizability tensor
at that dipole by its polarizability tensor  :
:
The Discrete Dipole Approximation (DDA) linear system is expressed as:

where  is the system matrix,
is the system matrix,  is the unknown polarization vector,
is the unknown polarization vector,  is the incident electric field vector. We have
is the incident electric field vector. We have
 .
.
 encodes interactions between dipoles via the Green's tensor (non-local), and
encodes interactions between dipoles via the Green's tensor (non-local), and  is a block-diagonal matrix with each block
is a block-diagonal matrix with each block  .
.
Let N be the number of dipoles. Each dipole has a polarization vector  . The total system is a matrix equation of size
. The total system is a matrix equation of size  :
:

Each block  is a
is a  complex matrix, defined by:
complex matrix, defined by:

So  is composed of
is composed of  blocks, each of size
blocks, each of size  .
.  is the inverse polarizability tensor,
is the inverse polarizability tensor,  is the dyadic Green's tensor for interaction between dipoles
is the dyadic Green's tensor for interaction between dipoles  and
and  ,
,  are the dipole polarization and incident electric field at dipole
are the dipole polarization and incident electric field at dipole  , respectively.
, respectively.
Typically dipoles are arranged on a regular grid. This implies translational invariance:

Because  , the matrix
, the matrix  is symmetric:
is symmetric:

Each dipole has three vector components ( ,
,  ,
,  ), so we can rearrange the unknown vector
), so we can rearrange the unknown vector  by grouping all x-components together, then y-components, then z-components:
by grouping all x-components together, then y-components, then z-components:

Similarly, the incident field can be grouped as:

Because the system is linear, we can equivalently rewrite it in block matrix form, that describe how the  -component of polarization affects the
-component of polarization affects the  -component of the resulting field:
-component of the resulting field:

The expanded form of the equations is:

Each block  and the total system size is
and the total system size is  . The interaction matrix
. The interaction matrix  is composed of 9 blocks:
is composed of 9 blocks:  (only 6 of them need to be evaluated due to symmetry). Each matrix-vector multiplication
(only 6 of them need to be evaluated due to symmetry). Each matrix-vector multiplication  can be computed as a convolution when the dipoles are arranged on a regular grid, allowing the use of Fast Fourier Transforms (FFTs) to accelerate the solution.
can be computed as a convolution when the dipoles are arranged on a regular grid, allowing the use of Fast Fourier Transforms (FFTs) to accelerate the solution.
Let  denote the inverse polarizability tensor for dipole
denote the inverse polarizability tensor for dipole  . Each
. Each  is a complex-valued
is a complex-valued  matrix. This gives:
matrix. This gives:



In the special case of an isotropic and homogeneous particle, the polarizabilities  are identical for all dipoles and proportional to the identity matrix:
are identical for all dipoles and proportional to the identity matrix:  . Then, the inverse becomes
. Then, the inverse becomes  , all off-diagonal elements vanish, and the expressions reduce to a simple element-wise division:
, all off-diagonal elements vanish, and the expressions reduce to a simple element-wise division:

Note on practical implementation. In Fortran and MATLAB, arrays such as  or
or  are stored in column-major order, where the first index varies fastest in memory (anti-lexicographic). This means that all x-components
are stored in column-major order, where the first index varies fastest in memory (anti-lexicographic). This means that all x-components  are contiguous in memory, followed by all y-components
are contiguous in memory, followed by all y-components  , and then all z-components
, and then all z-components  . In contrast, Python (NumPy) uses row-major order by default (lexicographic, last index varies fastest). To achieve the same contiguous layout of
. In contrast, Python (NumPy) uses row-major order by default (lexicographic, last index varies fastest). To achieve the same contiguous layout of  ,
,  ,
,  in memory, the array should be defined in Python as
in memory, the array should be defined in Python as  , with the vector component index (x, y, z) first. This ensures that
, with the vector component index (x, y, z) first. This ensures that  is stored contiguously in memory, followed by
is stored contiguously in memory, followed by  and
and  .
.