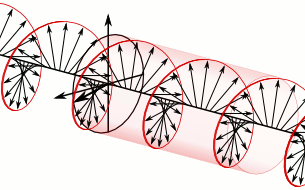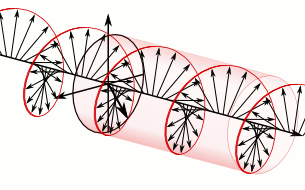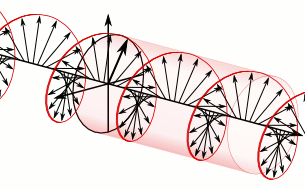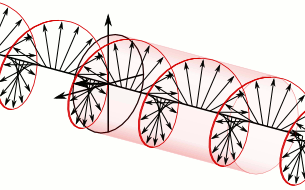
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to the direction of the wave.
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation. An elliptically polarized wave may be resolved into two linearly polarized waves in phase quadrature, with their polarization planes at right angles to each other. Since the electric field can rotate clockwise or counterclockwise as it propagates, elliptically polarized waves exhibit chirality.

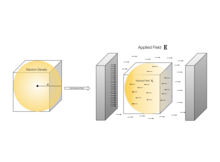
In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter ε (epsilon), is a measure of the electric polarizability of a dielectric material. A material with high permittivity polarizes more in response to an applied electric field than a material with low permittivity, thereby storing more energy in the material. In electrostatics, the permittivity plays an important role in determining the capacitance of a capacitor.
Physisorption, also called physical adsorption, is a process in which the electronic structure of the atom or molecule is barely perturbed upon adsorption.
Circular dichroism (CD) is dichroism involving circularly polarized light, i.e., the differential absorption of left- and right-handed light. Left-hand circular (LHC) and right-hand circular (RHC) polarized light represent two possible spin angular momentum states for a photon, and so circular dichroism is also referred to as dichroism for spin angular momentum. This phenomenon was discovered by Jean-Baptiste Biot, Augustin Fresnel, and Aimé Cotton in the first half of the 19th century. Circular dichroism and circular birefringence are manifestations of optical activity. It is exhibited in the absorption bands of optically active chiral molecules. CD spectroscopy has a wide range of applications in many different fields. Most notably, UV CD is used to investigate the secondary structure of proteins. UV/Vis CD is used to investigate charge-transfer transitions. Near-infrared CD is used to investigate geometric and electronic structure by probing metal d→d transitions. Vibrational circular dichroism, which uses light from the infrared energy region, is used for structural studies of small organic molecules, and most recently proteins and DNA.
Crystal optics is the branch of optics that describes the behaviour of light in anisotropic media, that is, media in which light behaves differently depending on which direction the light is propagating. The index of refraction depends on both composition and crystal structure and can be calculated using the Gladstone–Dale relation. Crystals are often naturally anisotropic, and in some media it is possible to induce anisotropy by applying an external electric field.

In classical electromagnetism, Ampère's circuital law relates the circulation of a magnetic field around a closed loop to the electric current passing through the loop.
The Kerr effect, also called the quadratic electro-optic (QEO) effect, is a change in the refractive index of a material in response to an applied electric field. The Kerr effect is distinct from the Pockels effect in that the induced index change for the Kerr effect is directly proportional to the square of the electric field instead of varying linearly with it. All materials show a Kerr effect, but certain liquids display it more strongly than others. The Kerr effect was discovered in 1875 by Scottish physicist John Kerr.

In classical electromagnetism, polarization density is the vector field that expresses the volumetric density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is said to be polarized.
In electricity (electromagnetism), the electric susceptibility is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field. The greater the electric susceptibility, the greater the ability of a material to polarize in response to the field, and thereby reduce the total electric field inside the material. It is in this way that the electric susceptibility influences the electric permittivity of the material and thus influences many other phenomena in that medium, from the capacitance of capacitors to the speed of light.
In electromagnetism, the Clausius–Mossotti relation, named for O. F. Mossotti and Rudolf Clausius, expresses the dielectric constant of a material in terms of the atomic polarizability, α, of the material's constituent atoms and/or molecules, or a homogeneous mixture thereof. It is equivalent to the Lorentz–Lorenz equation, which relates the refractive index of a substance to its polarizability. It may be expressed as:

In physics, the electric displacement field, also called electric flux density or electric induction, is a vector field that appears in Maxwell's equations. It accounts for the electromagnetic effects of polarization and that of an electric field, combining the two in an auxiliary field. It plays a major role in topics such as the capacitance of a material, as well as the response of dielectrics to an electric field, and how shapes can change due to electric fields in piezoelectricity or flexoelectricity as well as the creation of voltages and charge transfer due to elastic strains.
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system for three-dimensional Euclidean space, . Multipole expansions are useful because, similar to Taylor series, oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on , or less often on for some other .

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.

There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental interactions of nature. In this article, several approaches are discussed, although the equations are in terms of electric and magnetic fields, potentials, and charges with currents, generally speaking.
The hyperpolarizability, a nonlinear-optical property of a molecule, is the second order electric susceptibility per unit volume. The hyperpolarizability can be calculated using quantum chemical calculations developed in several software packages. See nonlinear optics.
When an electromagnetic wave travels through a medium in which it gets attenuated, it undergoes exponential decay as described by the Beer–Lambert law. However, there are many possible ways to characterize the wave and how quickly it is attenuated. This article describes the mathematical relationships among:

The electric dipole moment is a measure of the separation of positive and negative electrical charges within a system: that is, a measure of the system's overall polarity. The SI unit for electric dipole moment is the coulomb-metre (C⋅m). The debye (D) is another unit of measurement used in atomic physics and chemistry.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is thermal energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.

The Lorentz oscillator model describes the optical response of bound charges. The model is named after the Dutch physicist Hendrik Antoon Lorentz. It is a classical, phenomenological model for materials with characteristic resonance frequencies for optical absorption, e.g. ionic and molecular vibrations, interband transitions (semiconductors), phonons, and collective excitations.