A photon is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless, so they always move at the speed of light when in vacuum, 299792458 m/s. The photon belongs to the class of boson particles.

Compton scattering is the quantum theory of high frequency photons scattering following an interaction with a charged particle, usually an electron. Specifically, when the photon hits electrons, it releases loosely bound electrons from the outer valence shells of atoms or molecules.

The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, it is a characteristic of the system's total energy and momentum that is the same in all frames of reference related by Lorentz transformations. If a center-of-momentum frame exists for the system, then the invariant mass of a system is equal to its total mass in that "rest frame". In other reference frames, where the system's momentum is nonzero, the total mass of the system is greater than the invariant mass, but the invariant mass remains unchanged.

The Dirac sea is a theoretical model of the electron vacuum as an infinite sea of electrons with negative energy, now called positrons. It was first postulated by the British physicist Paul Dirac in 1930 to explain the anomalous negative-energy quantum states predicted by the Dirac equation for relativistic electrons. The positron, the antimatter counterpart of the electron, was originally conceived of as a hole in the Dirac sea, before its experimental discovery in 1932.

In physics, mass–energy equivalence is the relationship between mass and energy in a system's rest frame, where the two quantities differ only by a multiplicative constant and the units of measurement. The principle is described by the physicist Albert Einstein's formula: . In a reference frame where the system is moving, its relativistic energy and relativistic mass obey the same formula.
The word "mass" has two meanings in special relativity: invariant mass is an invariant quantity which is the same for all observers in all reference frames, while the relativistic mass is dependent on the velocity of the observer. According to the concept of mass–energy equivalence, invariant mass is equivalent to rest energy, while relativistic mass is equivalent to relativistic energy.

In physics, specifically relativistic quantum mechanics (RQM) and its applications to particle physics, relativistic wave equations predict the behavior of particles at high energies and velocities comparable to the speed of light. In the context of quantum field theory (QFT), the equations determine the dynamics of quantum fields. The solutions to the equations, universally denoted as ψ or Ψ, are referred to as "wave functions" in the context of RQM, and "fields" in the context of QFT. The equations themselves are called "wave equations" or "field equations", because they have the mathematical form of a wave equation or are generated from a Lagrangian density and the field-theoretic Euler–Lagrange equations.

In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the dispersion relation, one can calculate the frequency-dependent phase velocity and group velocity of each sinusoidal component of a wave in the medium, as a function of frequency. In addition to the geometry-dependent and material-dependent dispersion relations, the overarching Kramers–Kronig relations describe the frequency-dependence of wave propagation and attenuation.
In physics, the zitterbewegung (German pronunciation:[ˈtsɪtɐ.bəˌveːɡʊŋ], from German zittern 'to tremble, jitter', and Bewegung 'motion') is the theoretical prediction of a rapid oscillatory motion of elementary particles that obey relativistic wave equations. This prediction was first discussed by Gregory Breit in 1928 and later by Erwin Schrödinger in 1930 as a result of analysis of the wave packet solutions of the Dirac equation for relativistic electrons in free space, in which an interference between positive and negative energy states produces an apparent fluctuation (up to the speed of light) of the position of an electron around the median, with an angular frequency of 2mc2/ℏ, or approximately 1.6×1021 radians per second.
In physics, relativistic mechanics refers to mechanics compatible with special relativity (SR) and general relativity (GR). It provides a non-quantum mechanical description of a system of particles, or of a fluid, in cases where the velocities of moving objects are comparable to the speed of light c. As a result, classical mechanics is extended correctly to particles traveling at high velocities and energies, and provides a consistent inclusion of electromagnetism with the mechanics of particles. This was not possible in Galilean relativity, where it would be permitted for particles and light to travel at any speed, including faster than light. The foundations of relativistic mechanics are the postulates of special relativity and general relativity. The unification of SR with quantum mechanics is relativistic quantum mechanics, while attempts for that of GR is quantum gravity, an unsolved problem in physics.

In electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J. Larmor in 1897, in the context of the wave theory of light.
In physics, the energy–momentum relation, or relativistic dispersion relation, is the relativistic equation relating total energy to invariant mass and momentum. It is the extension of mass–energy equivalence for bodies or systems with non-zero momentum. It can be written as the following equation:
In 1929, physicist Oskar Klein obtained a surprising result by applying the Dirac equation to the familiar problem of electron scattering from a potential barrier. In nonrelativistic quantum mechanics, electron tunneling into a barrier is observed, with exponential damping. However, Klein's result showed that if the potential is at least of the order of the electron mass, , the barrier is nearly transparent. Moreover, as the potential approaches infinity, the reflection diminishes and the electron is always transmitted.
In the physics of electromagnetism, the Abraham–Lorentz force is the reaction force on an accelerating charged particle caused by the particle emitting electromagnetic radiation by self-interaction. It is also called the radiation reaction force, the radiation damping force, or the self-force. It is named after the physicists Max Abraham and Hendrik Lorentz.

Angle-resolved photoemission spectroscopy (ARPES) is an experimental technique used in condensed matter physics to probe the allowed energies and momenta of the electrons in a material, usually a crystalline solid. It is based on the photoelectric effect, in which an incoming photon of sufficient energy ejects an electron from the surface of a material. By directly measuring the kinetic energy and emission angle distributions of the emitted photoelectrons, the technique can map the electronic band structure and Fermi surfaces. ARPES is best suited for the study of one- or two-dimensional materials. It has been used by physicists to investigate high-temperature superconductors, graphene, topological materials, quantum well states, and materials exhibiting charge density waves.
In physics, relativistic quantum mechanics (RQM) is any Poincaré covariant formulation of quantum mechanics (QM). This theory is applicable to massive particles propagating at all velocities up to those comparable to the speed of light c, and can accommodate massless particles. The theory has application in high energy physics, particle physics and accelerator physics, as well as atomic physics, chemistry and condensed matter physics. Non-relativistic quantum mechanics refers to the mathematical formulation of quantum mechanics applied in the context of Galilean relativity, more specifically quantizing the equations of classical mechanics by replacing dynamical variables by operators. Relativistic quantum mechanics (RQM) is quantum mechanics applied with special relativity. Although the earlier formulations, like the Schrödinger picture and Heisenberg picture were originally formulated in a non-relativistic background, a few of them also work with special relativity.

A topological insulator is a material whose interior behaves as an electrical insulator while its surface behaves as an electrical conductor, meaning that electrons can only move along the surface of the material.
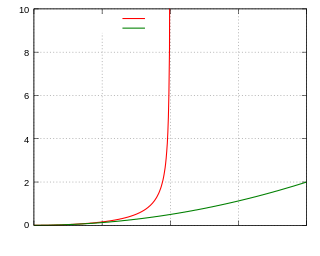
Tests of relativistic energy and momentum are aimed at measuring the relativistic expressions for energy, momentum, and mass. According to special relativity, the properties of particles moving approximately at the speed of light significantly deviate from the predictions of Newtonian mechanics. For instance, the speed of light cannot be reached by massive particles.

In physics, Dirac cones are features that occur in some electronic band structures that describe unusual electron transport properties of materials like graphene and topological insulators. In these materials, at energies near the Fermi level, the valence band and conduction band take the shape of the upper and lower halves of a conical surface, meeting at what are called Dirac points.
The term Dirac matter refers to a class of condensed matter systems which can be effectively described by the Dirac equation. Even though the Dirac equation itself was formulated for fermions, the quasi-particles present within Dirac matter can be of any statistics. As a consequence, Dirac matter can be distinguished in fermionic, bosonic or anyonic Dirac matter. Prominent examples of Dirac matter are graphene and other Dirac semimetals, topological insulators, Weyl semimetals, various high-temperature superconductors with -wave pairing and liquid helium-3. The effective theory of such systems is classified by a specific choice of the Dirac mass, the Dirac velocity, the gamma matrices and the space-time curvature. The universal treatment of the class of Dirac matter in terms of an effective theory leads to a common features with respect to the density of states, the heat capacity and impurity scattering.

















