Related Research Articles
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite matroid is equivalent to a geometric lattice.
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures.

Béla Bollobás FRS is a Hungarian-born British mathematician who has worked in various areas of mathematics, including functional analysis, combinatorics, graph theory, and percolation. He was strongly influenced by Paul Erdős since the age of 14.
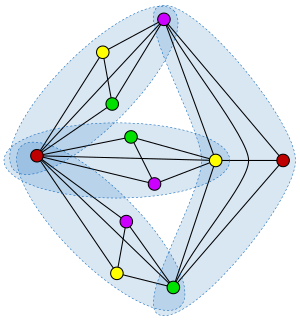
In graph theory, the Erdős–Faber–Lovász conjecture is a problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:

Paul D. Seymour is a British mathematician known for his work in discrete mathematics, especially graph theory. He was responsible for important progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture. Many of his recent papers are available from his website.

Jack R. Edmonds is an American-born and educated computer scientist and mathematician who lived and worked in Canada for much of his life. He has made fundamental contributions to the fields of combinatorial optimization, polyhedral combinatorics, discrete mathematics and the theory of computing. He was the recipient of the 1985 John von Neumann Theory Prize.

The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a graph polynomial. It is a polynomial in two variables which plays an important role in graph theory. It is defined for every undirected graph and contains information about how the graph is connected. It is denoted by .

Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra.

Geoffrey Richard GrimmettOLY is a mathematician known for his work on the mathematics of random systems arising in probability theory and statistical mechanics, especially percolation theory and the contact process. He is the Professor of Mathematical Statistics in the Statistical Laboratory, University of Cambridge, and was the Master of Downing College, Cambridge, from 2013 to 2018.
In matroid theory, the dual of a matroid is another matroid that has the same elements as , and in which a set is independent if and only if has a basis set disjoint from it.
Jon Hal Folkman was an American mathematician, a student of John Milnor, and a researcher at the RAND Corporation.
In matroid theory, an Eulerian matroid is a matroid whose elements can be partitioned into a collection of disjoint circuits.
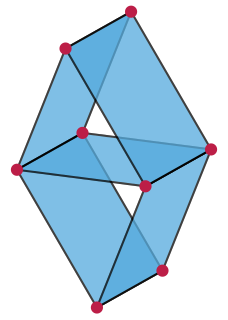
In the mathematical theory of matroids, a paving matroid is a matroid in which every circuit has size at least as large as the matroid's rank. In a matroid of rank every circuit has size at most , so it is equivalent to define paving matroids as the matroids in which the size of every circuit belongs to the set . It has been conjectured that almost all matroids are paving matroids.
Aubrey William Ingleton (1920–2000) was an English mathematician.
Algorithms and Combinatorics is a book series in mathematics, and particularly in combinatorics and the design and analysis of algorithms. It is published by Springer Science+Business Media, and was founded in 1987.
Hazel Perfect was a British mathematician specialising in combinatorics.

Henry Howland Crapo was an American-Canadian mathematician who worked in algebraic combinatorics. Over the course of his career, he held positions at several universities and research institutes in Canada and France. He is noted for his work in matroid theory and lattice theory.
Independence Theory in Combinatorics: An Introductory Account with Applications to Graphs and Transversals is an undergraduate-level mathematics textbook on the theory of matroids. It was written by Victor Bryant and Hazel Perfect, and published in 1980 by Chapman & Hall.
References
- ↑ Levens, R.G.C., ed. (1964). Merton College Register 1900-1964. Oxford: Basil Blackwell. p. 497.
- 1 2 3 4 Prof Dominic J A Welsh [ permanent dead link ], Debrett's, retrieved 2012-03-11.
- ↑ Oxley, James (2007), "The contributions of Dominic Welsh to matroid theory", in Grimmett, Geoffrey; McDiarmid, Colin (eds.), Combinatorics, Complexity, and Chance: A Tribute to Dominic Welsh (PDF), pp. 234–259, CiteSeerX 10.1.1.62.6989 , doi:10.1093/acprof:oso/9780198571278.003.0015, ISBN 9780198571278 .
- ↑ Dominic J. A. Welsh at the Mathematics Genealogy Project
- ↑ David R. Wood. "The Academic Family Tree of Dominic Welsh" (PDF).
- ↑ Review of Complexity and Cryptography by J. Rothe (2007), SIGACT News38 (2): 16–20, doi : 10.1145/1272729.1272735.